题目内容
⊙O的半径为6cm，弦AB的长为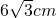
，以O为圆心，3cm长为半径作圆，与弦AB有________个公共交点．
1
分析：首先利用垂径定理即可求得AC的长，然后在直角△OAC中，利用勾股定理求得OC的长，再比较OC和3cm的大小即可．
解答：∵OC⊥AB，
∴AC=
AB=3
cm，
在直角△AOC中，OC=
=3cm，
∴OC=d=3cm，
∴以O为圆心，3cm长为半径作圆，与弦AB相切，
∴与弦AB有 1个公共交点，
故答案为1．
点评：本题考查了勾股定理以及垂径定理直线与圆的位置关系，正确求得OC的长是关键．
分析：首先利用垂径定理即可求得AC的长，然后在直角△OAC中，利用勾股定理求得OC的长，再比较OC和3cm的大小即可．
解答：∵OC⊥AB，
∴AC=
AB=3cm，在直角△AOC中，OC=
=3cm，∴OC=d=3cm，
∴以O为圆心，3cm长为半径作圆，与弦AB相切，
∴与弦AB有 1个公共交点，
故答案为1．
点评：本题考查了勾股定理以及垂径定理直线与圆的位置关系，正确求得OC的长是关键．
练习册系列答案
相关题目
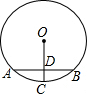（1997•新疆）如图，⊙O的半径为6cm，弦AB垂直平分半径OC于点D，则弦AB的长为