题目内容
10.若三角形的三角之比为1﹕2﹕3,则此三角形为直角三角形,且三角的对应边分别为c、a、b,则三边的关系为a2+b2=c2.分析 由三个内角之比,设出每一个内角,利用内角和定理列出方程,确定出三内角度数,即可确定出三角形的形状,根据三角形为直角三角形,利用勾股定理即可列出三边的关系.
解答 解:设三角形三内角度数分别为x,2x,3x,
根据题意得:x+2x+3x=180°,即6x=180°,
解得:x=30°,
∴三角形三内角分别为30°,60°,90°,
则三角形是直角三角形;
根据勾股定理得:a2+b2=c2.
故答案为:直角;a2+b2=c2.
点评 此题考查了直角三角形的性质,勾股定理,以及比例的性质,熟练掌握勾股定理的解本题的关键.

练习册系列答案
相关题目
5.下列函数中,y是x的反比例函数的是( )
| A. | y=x-1 | B. | y=$\frac{8}{{x}^{2}}$ | C. | $\frac{y}{x}$=2 | D. | y=$\frac{1}{2x}$ |
2.下列运算正确的是( )
| A. | $\sqrt{9}$=-3 | B. | |-3|=-3 | C. | -$\sqrt{-9}$=-3 | D. | -32=-9 |
19.(1)计算:${-1}^{2008}+2sin45°+(\frac{1}{2})^{-1}$
(2)化简:$\frac{a-1}{a-2}÷\frac{{a}^{2}-2a+1}{2a-4}$.
(2)化简:$\frac{a-1}{a-2}÷\frac{{a}^{2}-2a+1}{2a-4}$.
20.计算-2+3的结果是( )
| A. | -6 | B. | -5 | C. | -1 | D. | 1 |
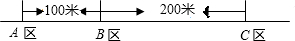 如图,某公司有三个住宅小区A,B,C,A,B,C各小区分别住有职工30人,15人,10人,且这三个小区在一条大道上(即A,B,C三点共线),已知AB=100米,BC=200米,为了方便职工上下班,该公司的接送车打算在某小区设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应该设在哪个小区?
如图,某公司有三个住宅小区A,B,C,A,B,C各小区分别住有职工30人,15人,10人,且这三个小区在一条大道上(即A,B,C三点共线),已知AB=100米,BC=200米,为了方便职工上下班,该公司的接送车打算在某小区设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应该设在哪个小区?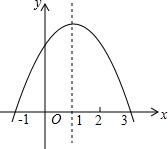 已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.
已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.