题目内容
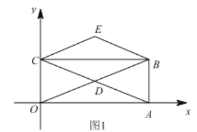
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() ,
,![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
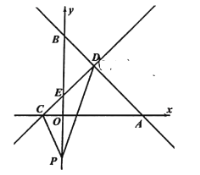
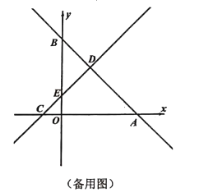
(1)若点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() 、
、![]() ,求当
,求当![]() 取最大值时,
取最大值时,![]() 点的坐标;
点的坐标;
(2)在(1)问的条件下,将![]() 沿
沿![]() 轴平移,在平移的过程中,直线
轴平移,在平移的过程中,直线![]() 交直线
交直线![]() 于点
于点![]() ,则当
,则当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
【答案】(1)P点坐标为![]() ;(2)BM的长为
;(2)BM的长为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将D点坐标代入![]() 求出m的值,然后求出C点坐标,作C点关于y轴的对称点C',连接DC',与y轴的交点即为点P,求出DC'直线解析式,即可求出P点坐标;
求出m的值,然后求出C点坐标,作C点关于y轴的对称点C',连接DC',与y轴的交点即为点P,求出DC'直线解析式,即可求出P点坐标;
(2)将![]() 代入直线
代入直线![]() ,求出b的值,再求A点坐标,设M点坐标为
,求出b的值,再求A点坐标,设M点坐标为![]() ,分三种情况讨论:①PA=PM,②PM=AM,③PA=AM,分别求出BM的长即可.
,分三种情况讨论:①PA=PM,②PM=AM,③PA=AM,分别求出BM的长即可.
(1)将![]() 代入
代入![]() 得:
得:![]()
∴![]()
当y=0时,![]() ,解得
,解得![]()
∴![]()
则![]() 关于y轴的对称点
关于y轴的对称点![]()
∴PC=PC',![]()
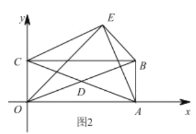
当P,C',D共线时,![]() 取得的最大值,如图所示,
取得的最大值,如图所示,
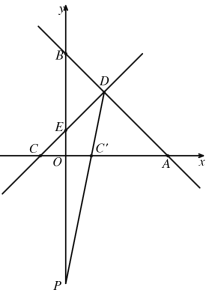
设直线PD解析式为![]() ,
,
将![]() ,
,![]() 代入得:
代入得:![]()
解得![]()
∴直线PD解析式为![]()
当x=0时,![]() ,
,
∴P点坐标为![]()
(2)将![]() 代入直线
代入直线![]() 得:
得:![]() ,
,
解得![]()
∴直线AB解析式为![]()
当y=0时,![]() ,解得
,解得![]() ,当x=0时,y=8
,当x=0时,y=8
∴A点坐标为![]() ,B点坐标为
,B点坐标为![]()
设M点坐标为![]()
①当PA=PM时,如图所示,
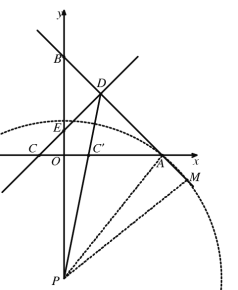
则![]()
解得![]() 或
或![]() (舍去)
(舍去)
此时M![]()
BM=![]()
②当PM=AM时,
则![]()
解得![]()
此时![]()
BM=![]()
③当PA=AM时,如图所示,
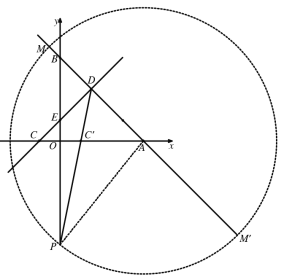
∵AB=![]() ,AM=AM'=PA=
,AM=AM'=PA=![]()
∴BM=AM-AB=![]() ,BM'=AM'+AB=
,BM'=AM'+AB=![]()
综上可得,BM的长为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目