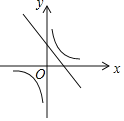ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌНЋвЛИіЕуЃЈКсзјБъгызнзјБъВЛЯрЕШЃЉЕФКсзјБъгызнзјБъЛЅЛЛКѓЕУЕНЕФЕуНазіетИіЕуЕФЁАЛЅЛЛЕуЁБЃЌШчЃЈЃ3ЃЌ5ЃЉгыЃЈ5ЃЌЃ3ЃЉЪЧвЛЖдЁАЛЅЛЛЕуЁБЁЃ
ЃЈ1ЃЉШЮвтвЛЖдЁАЛЅЛЛЕуЁБ________ЃЈЬюЁАЖМФмЁБЛђЁАЖМВЛФмЁБЃЉдквЛИіЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЛ
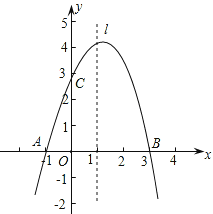
ЃЈ2ЃЉMЁЂNЪЧвЛЖдЁАЛЅЛЛЕуЁБЃЌШєЕуMЕФзјБъЮЊЃЈ2ЃЌЃ5ЃЉЃЌЧѓжБЯпMNЕФБэДяЪНЃЛ
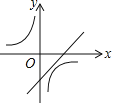
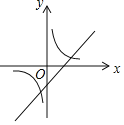
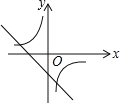
ЃЈ3ЃЉдкХзЮяЯп![]() ЕФЭМЯѓЩЯгавЛЖдЁАЛЅЛЛЕуЁБAЁЂBЃЌЦфжаЕуAдкЗДБШР§КЏЪ§
ЕФЭМЯѓЩЯгавЛЖдЁАЛЅЛЛЕуЁБAЁЂBЃЌЦфжаЕуAдкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌжБЯпABОЙ§ЕуPЃЈ
ЕФЭМЯѓЩЯЃЌжБЯпABОЙ§ЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЧѓДЫХзЮяЯпЕФБэДяЪН.
ЃЉЃЌЧѓДЫХзЮяЯпЕФБэДяЪН.
ЁОД№АИЁПЃЈ1ЃЉВЛвЛЖЈЃЛЃЈ2ЃЉy=ЃxЃ3ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
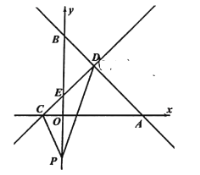
ЃЈ1ЃЉЩшетвЛЖдЁАЛЅЛЛЕуЁБЕФзјБъЮЊЃЈaЃЌbЃЉКЭЃЈbЃЌaЃЉЃЎЂйЕБab=0ЪБЃЌЫќУЧВЛПЩФмдкЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЌЂкЕБabЁй0ЪБЃЌгЩbЃН![]() ПЩЕУaЃН
ПЩЕУaЃН![]() ЃЌгкЪЧЕУЕННсТлЃЛ
ЃЌгкЪЧЕУЕННсТлЃЛ
ЃЈ2ЃЉАбMЃЈ2ЃЌ-5ЃЉЃЌNЃЈ-5ЃЌ2ЃЉДњШыy=cx+dЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉЩшЕуAЃЈpЃЌqЃЉЃЌдђqЃН![]() ЃЌгЩжБЯпABОЙ§ЕуPЃЈ
ЃЌгЩжБЯпABОЙ§ЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЕУЕНp+q=1ЃЌЕУЕНq=-1Лђq=2ЃЌНЋетвЛЖдЁАЛЅЛЛЕуЁБДњШыy=x2+bx+cЕУЃЌгкЪЧЕУЕННсТлЃЎ
ЃЉЃЌЕУЕНp+q=1ЃЌЕУЕНq=-1Лђq=2ЃЌНЋетвЛЖдЁАЛЅЛЛЕуЁБДњШыy=x2+bx+cЕУЃЌгкЪЧЕУЕННсТлЃЎ
ЃЈ1ЃЉВЛвЛЖЈЃЌ
ЩшетвЛЖдЁАЛЅЛЛЕуЁБЕФзјБъЮЊЃЈaЃЌbЃЉКЭЃЈbЃЌaЃЉЃЎ
ЂйЕБab=0ЪБЃЌЫќУЧВЛПЩФмдкЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЌ
ЂкЕБabЁй0ЪБЃЌгЩbЃН![]() ПЩЕУaЃН
ПЩЕУaЃН![]() ЃЌМДЃЈaЃЌbЃЉКЭЃЈbЃЌaЃЉЖМдкЗДБШР§КЏЪ§yЃН
ЃЌМДЃЈaЃЌbЃЉКЭЃЈbЃЌaЃЉЖМдкЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЛ
ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЛ
ЃЈ2ЃЉгЩMЃЈ2ЃЌ-5ЃЉЕУNЃЈ-5ЃЌ2ЃЉЃЌЩшжБЯпMNЕФБэДяЪНЮЊy=cx+dЃЈcЁй0ЃЉЃЎ
дђга![]()
НтЕУЃЌ![]() ЃЌ
ЃЌ
ЁржБЯпMNЕФБэДяЪНЮЊy=-x-3ЃЛ
ЃЈ3ЃЉЩшЕуAЃЈpЃЌqЃЉЃЌдђqЃН![]() ЃЌ
ЃЌ
ЁпжБЯпABОЙ§ЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌгЩЃЈ2ЃЉЕУ
ЃЉЃЌгЩЃЈ2ЃЉЕУ![]() ЃН
ЃН![]() +p+qЃЌ
+p+qЃЌ
Ёрp+q=1ЃЌ
Ёрp![]() ЃН1ЃЌ
ЃН1ЃЌ
НтВЂМьбщЕУЃКp=2Лђp=-1ЃЌ
Ёрq=-1Лђq=2ЃЌ
ЁретвЛЖдЁАЛЅЛЛЕуЁБЪЧЃЈ2ЃЌ-1ЃЉКЭЃЈ-1ЃЌ2ЃЉЃЌ
НЋетвЛЖдЁАЛЅЛЛЕуЁБДњШыy=x2+bx+cЕУЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрДЫХзЮяЯпЕФБэДяЪНЮЊy=x2-2x-1ЃЎ

 ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИ
ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИ