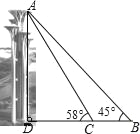
题目内容
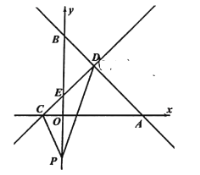
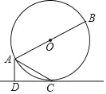
【题目】已知:如图,AB为⊙O的直径,AC是⊙O的弦,AD垂直于过点C的直线DC,垂足为点D,且AC平分∠BAD.
(1)求证:CD是⊙O的切线;
(2)若AD=1,AB=5,求AC的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OC,由题意知∠DAC=∠OAC=∠OCA,据此得AD∥OC,根据AD⊥DC即可得证;
(2)连接BC,证△ADC∽△ACB即可得.
解:(1)如图,连接OC,

∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAO,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥DC,
∴OC⊥DC,
∴CD是⊙O的切线;
(2)连接BC,
∵AB是⊙O的直径,AD⊥DC,
∴∠ADC=∠ACB=90°,
又∵∠DAC=∠CAB,
∴△ADC∽△ACB,
则![]() =
=![]() ,即AC2=ADAB,
,即AC2=ADAB,
∵AD=1、AB=5,
∴AC2=5,
则AC=![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目