题目内容
某次竞赛满分为100分，有六个学生的得分彼此不等，依次按高分到低分排列名次．他们六个人的平均分为91分，第六名的得分是65分．则第三名的得分至少是
95
95
分．分析：设六个人的成绩依次为x1，x2，x3，x4，x5，x6，则65=x6＜x5＜x4＜x3＜x2＜x1≤100，x1+x2+x3+x4+x5=546-65=481，要使x3最小，必须x1，x2尽可能大，x4，x5尽可能接近x3，继而求解即可．
解答：解：设六个人的成绩依次为x1，x2，x3，x4，x5，x6，则65=x6＜x5＜x4＜x3＜x2＜x1≤100
由
（x1+x2+x3+x4+x5+x6）=91，得出：x1+x2+x3+x4+x5+x6=546，
∴x1+x2+x3+x4+x5=546-65=481．
要使x3最小，必须x1，x2尽可能大，x4，x5尽可能接近x3，
所以当x1=100，x2=99，x4=x3-1，x5=x3-2时，x3取最小值，
即100+99+x3+（x3-1）+（x3-2）=481．
3x3=481-100-99+3=285．
解答：x3=95．
答：第三名的得分至少是9（5分）．
由
| 1 |
| 6 |
∴x1+x2+x3+x4+x5=546-65=481．
要使x3最小，必须x1，x2尽可能大，x4，x5尽可能接近x3，
所以当x1=100，x2=99，x4=x3-1，x5=x3-2时，x3取最小值，
即100+99+x3+（x3-1）+（x3-2）=481．
3x3=481-100-99+3=285．
解答：x3=95．
答：第三名的得分至少是9（5分）．
点评：本题考查的是应用类问题，解题关键是得出使x3最小，必须x1，x2尽可能大，x4，x5尽可能接近x3，有一定难度．
练习册系列答案
相关题目
为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，并从中随机抽取了部分学生成绩（得分取整数，满分为100分）为样本，绘制成统计图（如图所示），请根据统计图提供的信息回答下列问题：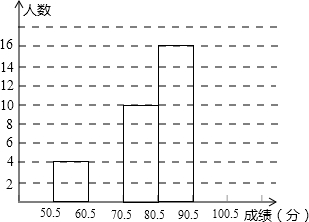
分为100分）进行统计．请你根据尚未完成并有局部污染的频率分布表和频率分布直方图，解答下列问题：