题目内容
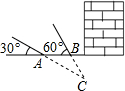
探测队探测出某建筑物下面有文物,为了准确测出文物所在的深度,在地面上相距20米的A,B两处,用仪器探测文物C,探测线与地面的夹角分别是30°和60°(如图所示).(1)画出表示文物C深度的线段CD;
(2)求出该文物所在位置的深度.

【答案】分析:(1)过C向地面引垂线,垂线段即为文物深度;
(2)CD既在△BCD中,又在△ACD中,所以可借助两个直角三角形进行解题.设CD=x,在Rt△BDC中,利用60°角的正切可知BD=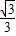 x,进而表示出AD长,在Rt△ACD中,利用∠A=30°且tan30°=
x,进而表示出AD长,在Rt△ACD中,利用∠A=30°且tan30°=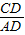 即列方程可得
即列方程可得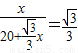 ,解方程即可.
,解方程即可.
解答: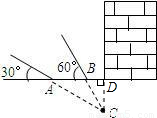 解:(1)过C作AB延长线的垂线CD,垂足为D,则CD即为所求;
解:(1)过C作AB延长线的垂线CD,垂足为D,则CD即为所求;
(2)假设CD=x,在Rt△BDC中,∠DBC=60°,且tan60°= ,
,
∴BD=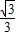 x,
x,
∵AB=20,
∴AD=20+ x,
x,
在Rt△ACD中,
∵∠A=30°且tan30°=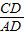 ,
,
即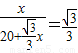 ,
,
∴x=10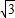 .
.
∴文物所在位置的深度10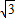 米.
米.
点评:解此题的关键是把实际问题转化为数学问题,把实际问题抽象到解直角三角形中,利用公共边及相应的三角函数求解.
(2)CD既在△BCD中,又在△ACD中,所以可借助两个直角三角形进行解题.设CD=x,在Rt△BDC中,利用60°角的正切可知BD=
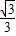 x,进而表示出AD长,在Rt△ACD中,利用∠A=30°且tan30°=
x,进而表示出AD长,在Rt△ACD中,利用∠A=30°且tan30°=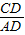 即列方程可得
即列方程可得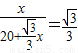 ,解方程即可.
,解方程即可.解答:
 解:(1)过C作AB延长线的垂线CD,垂足为D,则CD即为所求;
解:(1)过C作AB延长线的垂线CD,垂足为D,则CD即为所求;(2)假设CD=x,在Rt△BDC中,∠DBC=60°,且tan60°=
 ,
,∴BD=
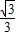 x,
x,∵AB=20,
∴AD=20+
 x,
x,在Rt△ACD中,
∵∠A=30°且tan30°=
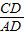 ,
,即
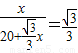 ,
,∴x=10
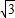 .
.∴文物所在位置的深度10
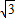 米.
米.点评:解此题的关键是把实际问题转化为数学问题,把实际问题抽象到解直角三角形中,利用公共边及相应的三角函数求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
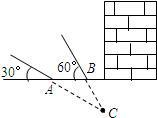 的A,B两处,用仪器探测文物C,探测线与地面的夹角分别是30°和60°(如图所示).
的A,B两处,用仪器探测文物C,探测线与地面的夹角分别是30°和60°(如图所示). 在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值).
在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值). 文物探测队探测出某建筑物下面有地下文物,为了准确测出文物所在的深度,他们在文物上方建筑物的一侧地面上相距20米的A、B两处,用仪器测文物C,探测线与地面的夹角分别是30°和60°,求该文物所在位置的深度(精确到0.1米).
文物探测队探测出某建筑物下面有地下文物,为了准确测出文物所在的深度,他们在文物上方建筑物的一侧地面上相距20米的A、B两处,用仪器测文物C,探测线与地面的夹角分别是30°和60°,求该文物所在位置的深度(精确到0.1米).