题目内容
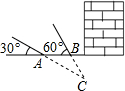
 在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值).
在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值).分析:过C点作AB的垂线交AB的延长线于点D,由三角形外角的性质可得出∠ACB=30°,进而可得出BC=AB=5米,在Rt△CDB中利用锐角三角函数的定义即可求出CD的值
解答:解:过C点作AB的垂线交AB的延长线于点D,
∵∠CAD=30°,∠CBD=60°,
∴∠ACB=30°,
∴∠CAB=∠ACB=30°,
∴BC=AB=5米,
在Rt△CDB中,BC=5米,∠CBD=60°,sin∠CBD=
,
∴sin60°=
,
∴CD=3sin60°=5×
=
(米),
答:该生命迹象所在位置的深度为
.
∵∠CAD=30°,∠CBD=60°,
∴∠ACB=30°,

∴∠CAB=∠ACB=30°,
∴BC=AB=5米,
在Rt△CDB中,BC=5米,∠CBD=60°,sin∠CBD=
| CD |
| BC |
∴sin60°=
| CD |
| 3 |
∴CD=3sin60°=5×
| ||
| 2 |
5
| ||
| 2 |
答:该生命迹象所在位置的深度为
5
| ||
| 2 |
点评:本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值).
在玉树地震抢救中,某武警部队探测队探测出某建筑物下面有生命迹象,为了准确测出生命迹象所在的深度,他们在生命迹象上方建筑物的一侧地面上相距5米的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(结果取准确值).