Question

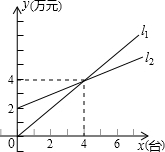
如图，l₁表示名湖商场一天的彩电销售额与销售量的关系，l₂表示该公司一天的销售成本与彩电销售量的关系．
①x=2时，销售额=

8

3

万元，销售成本=

10

3

万元．利润（收入-成本）=

-

2

3

万元．
②一天销售

3

件时，销售额等于销售成本．
③l₁对应的函数表达式是

l₁=

4

3

x

．
④写出利润与销售量间的函数表达式．

Answer 1

分析：①由图象可知，两图象都经过（3，4）点，利用待定系数法求一次函数解析式，进而得出当x=2时，l₁，l₂，的值即可，得出此时销售额与销售成本，求出利润，
②两直线的交点为（3，4），即销售3台时，销售额=销售成本，进而得出答案．
③因为x=3时，y=4，图象过原点，所以l₁=

4

3

x，
④可得，l₁=

4

3

x，l₂=

2

3

x+2，所以利润与销售量之间的解析式是W=l₁-l₂得出答案即可．

解答：解：①将（3，4）代入l₁=kx得：4=3k，
解得：k=

4

3

，
故l₁=

4

3

x，
则x=2时，l₁=

8

3

，
设l₂=ax+b，将（3，4），（0，2）代入得出：

b=2 3a+b=4

，
解得：

a= 2 3 b=2

，
故l₂=

2

3

x+2，
当x=2时，l₂=

10

3

，
当x=2时，利润（收入-成本）=

8

3

-

10

3

=-

2

3

，
故答案为：

8

3

，

10

3

，-

2

3

；

②根据图象可得出，一天销售等于3件时，销售额等于销售成本．
故答案为：3；

③根据①得出l₁对应的函数表达式是：l₁=

4

3

x；
故答案为：l₁=

4

3

x；

④设利润为：W=l₁-l₂=

4

3

x-（

2

3

x+2）=

2

3

x-2．

点评：本题考查了一次函数的图象和性质以及一次函数的应用，理解两函数图象的交点的意义是解题的关键．