题目内容
 如图,△ABC与以AB为直径的⊙O相交于点D,且点D为AC中点,点F是⊙O的切线BC延长线上的一点,连结FD并延长与⊙O相交于点E,DG⊥BC于点G.
如图,△ABC与以AB为直径的⊙O相交于点D,且点D为AC中点,点F是⊙O的切线BC延长线上的一点,连结FD并延长与⊙O相交于点E,DG⊥BC于点G.(1)求证:DG为⊙O的切线;
(2)当∠F=15°,AE=3时,求⊙O半径.
考点:切线的判定与性质
专题:
分析:(1)连结OD,由BC是⊙O的切线就可以得出AB⊥BC,∠ABC=90°,DG⊥BC,就可以得出DG∥AB,D为AC中点,就有DG=GC,DG=
AB,OD是△ABC的中位线,就可以得出OD∥BC,就可以得出∠BOD=90°,就可以得出∠GDO=90°,得出结论;
(2)连结OE,由OD∥BC就可以得出∠AOD=90°,∠ADO=∠ACB,由OA=OD就可以得出∠ADO=45°,得出∠ACB=45°,由外角与内角的关系就可以得出∠CDF=30°,进而得出∠ADE=30°,就有∠AOE=60°,AO=EO得出△AEO为等边三角形,就可以得出结论.
| 1 |
| 2 |
(2)连结OE,由OD∥BC就可以得出∠AOD=90°,∠ADO=∠ACB,由OA=OD就可以得出∠ADO=45°,得出∠ACB=45°,由外角与内角的关系就可以得出∠CDF=30°,进而得出∠ADE=30°,就有∠AOE=60°,AO=EO得出△AEO为等边三角形,就可以得出结论.
解答:解:(1)连结OD,
∵点D为AC中点,O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∴∠AOD=∠B,∠ADO=∠ACB.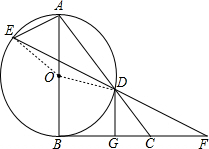
∵BC是⊙O的切线,
∴AB⊥BC,
∴∠ABC=90°,
∴∠AOD=90°,
∴∠BOD=90°.
∵DG⊥BC,
∴∠DGB=90°.
∵∠DOB+∠B+∠DGB+∠GDO=360°,
∴∠GDO=90°,
∴GD⊥OD.
∴DG为⊙O的切线;
(2)∵∠AOD=90°,AO=DO,
∴∠ADO=45°,
∴∠ACB=45°.
∵∠ACB=∠F+∠CDF,且∠F=15°,
∴45°=15°+∠CDF,
∴∠CDF=30°,
∴∠ADE=30°.
∵∠AOE=2∠ADE,
∴∠AOE=60°.
∵AO=EO,
∴△AOE是等边三角形.
∴AO=AE.
∵AE=3,
∴AO=3,
∴⊙O半径为3.
∵点D为AC中点,O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∴∠AOD=∠B,∠ADO=∠ACB.

∵BC是⊙O的切线,
∴AB⊥BC,
∴∠ABC=90°,
∴∠AOD=90°,
∴∠BOD=90°.
∵DG⊥BC,
∴∠DGB=90°.
∵∠DOB+∠B+∠DGB+∠GDO=360°,
∴∠GDO=90°,
∴GD⊥OD.
∴DG为⊙O的切线;
(2)∵∠AOD=90°,AO=DO,
∴∠ADO=45°,
∴∠ACB=45°.
∵∠ACB=∠F+∠CDF,且∠F=15°,
∴45°=15°+∠CDF,
∴∠CDF=30°,
∴∠ADE=30°.
∵∠AOE=2∠ADE,
∴∠AOE=60°.
∵AO=EO,
∴△AOE是等边三角形.
∴AO=AE.
∵AE=3,
∴AO=3,
∴⊙O半径为3.
点评:本题考查了切线的判定及性质的运用,三角形的中位线的判定及性质的运用,三角形的外角与内角的关系的运用,圆心角与圆周角的关系的运用,等边三角形的判定及性质的运用,解答时运用切线的性质求解是关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
下列计算正确的是( )
| A、3m2-2m2=1 |
| B、3m2+2m2=5m4 |
| C、3m2n-3m2n=0 |
| D、3m+2n=5mn |
 已知如图所示,
已知如图所示,
 如图,折叠矩形纸片ABCD,得折痕BD,再折叠AD使点A与点F重合,折痕为DG,若AB=4,BC=3,求AG的长.
如图,折叠矩形纸片ABCD,得折痕BD,再折叠AD使点A与点F重合,折痕为DG,若AB=4,BC=3,求AG的长.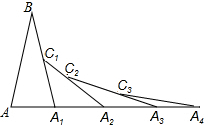 如图,已知AB=A1B,A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…按这样的方式继续下去,若∠B=20°,则∠A4=
如图,已知AB=A1B,A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…按这样的方式继续下去,若∠B=20°,则∠A4=