题目内容
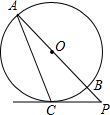如图，PC切⊙O于点C，射线PO分别交⊙O于点A、B，∠A=20°，则∠P=________°．
50
分析：连接OC，利用同弧所对的圆周角等于所对圆心角的一半求出∠COP的度数，由PC为圆O的切线，利用切线的性质得到OC垂直于CP，在直角三角形OPC中，利用直角三角形的两锐角互余即可求出∠P的度数．
解答：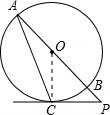
解：连接OC，
∵∠A与∠COP都对
，且∠A=20°，
∴∠COP=40°，
∵CP与圆O相切，
∴OC⊥CP，
在Rt△COP中，
∠P=90°-∠COP=50°．
故答案为：50
点评：此题考查了切线的性质，圆周角定理，以及直角三角形的性质，熟练掌握切线的性质是解本题的关键．
分析：连接OC，利用同弧所对的圆周角等于所对圆心角的一半求出∠COP的度数，由PC为圆O的切线，利用切线的性质得到OC垂直于CP，在直角三角形OPC中，利用直角三角形的两锐角互余即可求出∠P的度数．
解答：
解：连接OC，∵∠A与∠COP都对
，且∠A=20°，∴∠COP=40°，
∵CP与圆O相切，
∴OC⊥CP，
在Rt△COP中，
∠P=90°-∠COP=50°．
故答案为：50
点评：此题考查了切线的性质，圆周角定理，以及直角三角形的性质，熟练掌握切线的性质是解本题的关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
已知：如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC=4，PB=8，则PA=
如图，PC切⊙O于点C，过圆心的割线PAB交⊙O于A、B两点，BE⊥PE，垂足为E，BE交⊙O于点D，F是PC上一点，且PF=AF，FA的延长线交⊙O于点G．求证：
（1998•大连）如图，PC切⊙O于点C，割线PAB交⊙O于点A、B，若PA=2，AB=4，则BC2：AC2的值为（ ）
如图，PC切⊙O于点C，PA过点O且交⊙O于点A，B，若PC=6cm，PB=4cm，则⊙O的半径为