题目内容
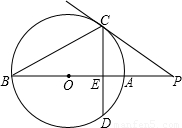
已知：如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC=4，PB=8，则PA=分析：先根据切割线定理求得PA，从而可得到半径的长；
根据已知即可求得三角函数的值；
根据三角形的面积公式可求得CE的长，从而也就得到了CD的长．
根据已知即可求得三角函数的值；
根据三角形的面积公式可求得CE的长，从而也就得到了CD的长．
解答：
解：∵PC切⊙O于点C，割线PAB经过圆心O，PC=4，PB=8，
∴PC2=PA•PB．
∴PA=
=2．
∴AB=6．
∴圆的半径是3．
连接OC．
∵OC=3，OP=5，
∴sin∠P=
．
∴CE=
，
∴CD=
．
解：∵PC切⊙O于点C，割线PAB经过圆心O，PC=4，PB=8，∴PC2=PA•PB．
∴PA=
| 16 |
| 8 |
∴AB=6．
∴圆的半径是3．
连接OC．
∵OC=3，OP=5，
∴sin∠P=
| 3 |
| 5 |
∴CE=
| 12 |
| 5 |
∴CD=
| 24 |
| 5 |
点评：综合运用了切割线定理、锐角三角形函数的定义、垂径定理．
练习册系列答案
相关题目
已知：如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC=4，PB=8，则PA=________，sin∠P=________，CD=________．
