题目内容
18. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
分析 由图可知:两个一次函数的交点坐标为(-3,1);那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
解答 解:函数y=ax+b和y=kx的图象交于点P(-3,1),
即x=-3,y=1同时满足两个一次函数的解析式.
所以关于x,y的方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$.
故选C.
点评 本题考查了一次函数与二元一次方程组,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
相关题目
3.要使分式$\frac{3}{x-2}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≠-2 | D. | x≠2 |
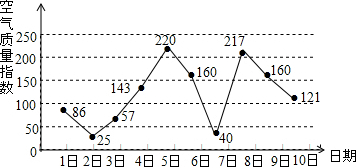
6.如图是某市某月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留3天.则此人在该市停留期间有且仅有1天空气质量重度污染的概率是( )

| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个.
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个. 如图,四边形ABCD是⊙O的内接四边形,若⊙O的半径为3cm,∠A=110°,则劣弧$\widehat{BD}$的长为$\frac{7π}{3}$cm.
如图,四边形ABCD是⊙O的内接四边形,若⊙O的半径为3cm,∠A=110°,则劣弧$\widehat{BD}$的长为$\frac{7π}{3}$cm.