题目内容
6.如图是某市某月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留3天.则此人在该市停留期间有且仅有1天空气质量重度污染的概率是( )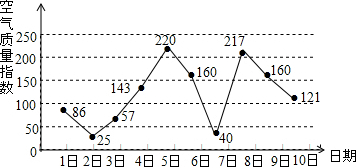
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 先求出3天中空气质量指数的所有情况,再求出1天空气质量为重度污染的情况数,根据概率公式求解即可.
解答 解:∵由图可知,当1号到达时,停留的日子为1、2、3号,此时为(86,25,57),3天空气质量均为优;
当2号到达时,停留的日子为2、3、4号,此时为(25,57,143),2天空气质量为优;
当3号到达时,停留的日子为3、4、5号,此时为(57,143,220),1天空气质量为重度污染;
当4号到达时,停留的日子为4、5、6号,此时为(143,220,160),1天空气质量为重度污染;
当5号到达时,停留的日子为5、6、7号,此时为(220,160,40),1天空气质量为重度污染;
当6号到达时,停留的日子为6、7、8号,此时为(160,40,217),1天空气质量为重度污染;
当7号到达时,停留的日子为7、8、9号,此时为(40,217,160),1天空气质量为重度污染;
当8号到达时,停留的日子为8、9、10号,此时为(217,160,121),1天空气质量为重度污染;
∴此人在该市停留期间有且仅有1天空气质量为重度污染的概率=$\frac{6}{8}$=$\frac{3}{4}$.
故选:D.
点评 本题考查的是概率公式,熟知随机事件A的概率P(A)=事件A可能出现的结果数与所有可能出现的结果数的商是解答此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
11.已知一个正多边形的每个外角等于60°,则这个正多边形是( )
| A. | 正五边形 | B. | 正六边形 | C. | 正七边形 | D. | 正八边形 |
14. 几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )
几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )
 几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )
几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
18. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是( )
 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
16.若关于x的方程2x-m=x-2的解为x=3,则m的值为( )
| A. | -5 | B. | 5 | C. | -7 | D. | 7 |




 如图,抛物线y=ax2+bx+c为x轴的一交点为A(-6,0),与y轴的交点为C(0,3),且经过点G(-2,3).
如图,抛物线y=ax2+bx+c为x轴的一交点为A(-6,0),与y轴的交点为C(0,3),且经过点G(-2,3).