Question

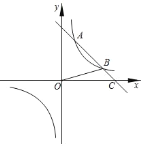
【题目】如下图所示，在直角坐标系中，以为圆心的与轴相交于两点，与轴相交于两点，连接．

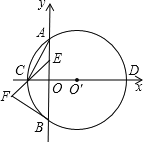
（1）上有一点，使得．求证；

（2）在（1）的结论下，延长到点，连接，若，请证明与相切；

（3）如果，的半径为2，求（2）中直线的解析式．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】

（1）通过证明∽即可得证；

（2）连接，关键证明，从而易得，得到与相切；

（3）由，的半径为2，易得，均为等边三角形，它们的高分别是，从而易得点B，P的坐标，由待定系数法求出直线的解析式．

解：（1）由题意可知，，

又因为，所以，

故∽，

所以，

（2）连接，则，

因为，，

故，

即，所以与相切．

（3），，所以，

，

所以，均为等边三角形，它们的高分别是，

故点的坐标为；点的横坐标为，纵坐标为，

设的直线为，则，

所以，所以直线的解析式为．