题目内容
解方程：4（x-1）2=9（2x+3）2．
考点：解一元二次方程-直接开平方法
专题：
分析：先移项，使等式右边为0，再运用平方差公式分解左边，使每一因式为0，求解即可．
解答：解：移项，得4（x-1）2-9（2x+3）2=0，
分解因式，得[2（x-1）+3（2x+3）][2（x-1）-3（2x+3）]=0，
即（10x+7）（-4x-11）=0，
所以10x+7=0或-4x-11=0，
解得x1=-
，x2=-
．
分解因式，得[2（x-1）+3（2x+3）][2（x-1）-3（2x+3）]=0，
即（10x+7）（-4x-11）=0，
所以10x+7=0或-4x-11=0，
解得x1=-
| 7 |
| 10 |
| 11 |
| 4 |
点评：本题考查了解一元二次方程的方法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．
练习册系列答案
相关题目
⊙O的半径为4，圆心到点P的距离为d，且d是方程x2-2x-8=0的根，则点P与⊙O的位置关系是（ ）
| A、点P在⊙O内部 |
| B、点P在⊙O上 |
| C、点P在⊙O外部 |
| D、点P不在⊙O上 |
如果一个多项式是五次多项式，那么（ ）
| A、这个多项式至少有一项的次数是5 |
| B、这个多项式只能有一项的次数是5 |
| C、这个多项式一定是五次六项式 |
| D、这个多项式最多有六项 |
已知．在Rt△OAB中，∠OAB=90°，∠BOA=30°，OA=2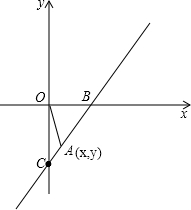
如图，y=2x-1与x轴、y轴分别交于B、C两点，点A（x，y）是第四象限内的直线y=2x-1上的一个动点．