题目内容
11.如图,已知直线AB与正比例函数y=kx(k≠0)的图象交于点A(5,5),与x轴交于点B(-$\frac{5}{2}$,0).点P为直线OA上的动点,点P的横坐标为t,以点P为顶点,作矩形PDEF,满足PD∥x轴,且PD=1,PF=2.
(1)求k值及直线AB的函数表达式;并判定t=1时点E是否落在直线AB上,请说明理由;
(2)在点P运动的过程中,当点F落在直线AB上时,求t的值;
(3)在点P运动的过程中,若矩形PDEF与直线AB有公共点,求t的取值范围.
分析 (1)根据待定系数法即可求得k值及直线AB的函数表达式,然后根据题意求得E的坐标,当然直线AB的解析式即可判断E在直线AB上;
(2)根据直线OA的解析式得出P的坐标,根据题意求得F的坐标,当然直线AB的解析式,即可求得t的值;
(3)表示出D的坐标,代入直线AB的解析式,求得t的值,再结合(1)即可求得矩形PDEF与直线AB有公共点时的t的取值范围.
解答 解:(1)∵直线AB与正比例函数y=kx(k≠0)的图象交于点A(5,5),与x轴交于点B(-$\frac{5}{2}$,0).
设直线AB的解析式为y=mx+n,
∴5=5k,$\left\{\begin{array}{l}{5m+n=5}\\{-\frac{5}{2}m+n=0}\end{array}\right.$,
解得k=1,$\left\{\begin{array}{l}{m=\frac{2}{3}}\\{n=\frac{5}{3}}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{2}{3}$x+$\frac{5}{3}$;
∵点P为直线OA上的动点,点P的横坐标为t=1,
∴E(2,3),
把x=2,y=3代入y=$\frac{2}{3}$x+$\frac{5}{3}$中成立,
∴点E落在直线AB上;
(2)∵点P为直线OA上,∴P(t,t),
∴F(t,t+2),
把F(t,t+2)代入y=$\frac{2}{3}$x+$\frac{5}{3}$中得t+2=$\frac{2}{3}$t+$\frac{5}{3}$,解得t=-1;
(3)∵P(t,t),
∴D(t+1,t),把D(t+1,t)代入y=$\frac{2}{3}$x+$\frac{5}{3}$中得t=$\frac{2}{3}$(t+1)+$\frac{5}{3}$,解得t=7,
∴若矩形PDEF与直线AB有公共点,t的取值范围为-1≤t≤7.
点评 本题是一次函数的综合题,考查了待定系数法求一次函数的解析式,图象上点的坐标特征,矩形的性质等,根据题意表示出D、E、F点的坐标是解题的关键.

| A. | 1.22×106 | B. | 0.122×107 | C. | 122×104 | D. | 1.2×106 |
| A. | n(n+2) | B. | (-1)nn(n+2) | C. | (-1)n(n2-1) | D. | -n(n+1) |
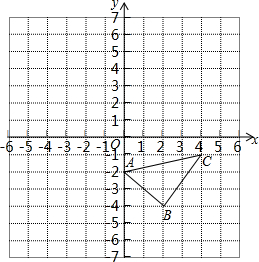 如图,在平面直角坐标系中,△ABC的三个顶点均在格点上.
如图,在平面直角坐标系中,△ABC的三个顶点均在格点上. 如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.
如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.