题目内容
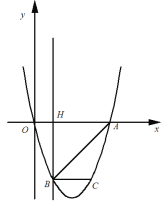
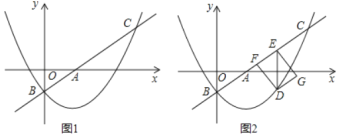
【题目】如图1,在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 的另一个交点为
的另一个交点为![]() .
.
(1)求![]() 的值和抛物线的解析式;
的值和抛物线的解析式;
(2)点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标为
的横坐标为![]() (
(![]() ).
).![]() 轴交直线
轴交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且四边形
上,且四边形![]() 为矩形(如图2),若矩形
为矩形(如图2),若矩形![]() 的周长为
的周长为![]() ,求
,求![]() 与
与![]() 的函数关系式以及
的函数关系式以及![]() 的最大值;
的最大值;
(3)![]() 是平面内一点,将
是平面内一点,将![]() 绕点
绕点![]() 沿逆时针方向旋转
沿逆时针方向旋转![]() 后,得到
后,得到![]() ,点
,点![]() 、
、![]() 、
、![]() 的对应点分别是点
的对应点分别是点![]() 、
、![]() 、
、![]() .若
.若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ,抛物线的解析式为
,抛物线的解析式为![]() ;(2)
;(2)![]() ,
,![]() 有最大值
有最大值![]() ;(3)点
;(3)点![]() 的横坐标为
的横坐标为![]() 或
或![]() .
.
【解析】
(1)把点B的坐标代入直线解析式求出m的值,再把点C的坐标代入直线求解即可得到n的值,然后利用待定系数法求二次函数解析式解答;
(2)令y=0求出点A的坐标,从而得到OA、OB的长度,利用勾股定理列式求出AB的长,然后根据两直线平行,内错角相等可得∠ABO=∠DEF,再解直角三角形用DE表示出EF、DF,根据矩形的周长公式表示出p,利用直线和抛物线的解析式表示DE的长,整理即可得到P与t的关系式,再利用二次函数的最值问题解答;
(3)根据逆时针旋转角为90°可得A1O1∥y轴时,B1O1∥x轴,然后分①点O1、B1在抛物线上时,表示出两点的横坐标,再根据纵坐标相同列出方程求解即可;②点A1、B1在抛物线上时,表示出点B1的横坐标,再根据两点的纵坐标相差A1O1的长度列出方程求解即可.
(1)∵直线![]() :
:![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∵直线![]() :
:![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∵抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
∴ ,解得
,解得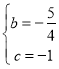 ,
,
∴抛物线的解析式为![]() ;
;
(2)令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴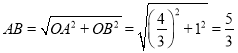 ,
,
∵![]() 轴,
轴,
∴![]() ,
,
在矩形![]() 中,
中,![]() ,
,
![]() ,
,
∴![]() ,
,
∵点![]() 的横坐标为
的横坐标为![]() (
(![]() ),
),
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ;
;
(3)∵![]() 绕点
绕点![]() 沿逆时针方向旋转
沿逆时针方向旋转![]() ,
,
∴![]() 轴时,
轴时,![]() 轴,设点
轴,设点![]() 的横坐标为
的横坐标为![]() ,
,
①如图1,点![]() 、
、![]() 在抛物线上时,点
在抛物线上时,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,
,
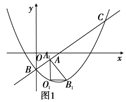
∴![]() ,
,
解得![]() ,
,
②如图2,点![]() 、
、![]() 在抛的线上时,点
在抛的线上时,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的纵坐标比点
的纵坐标比点![]() 的纵坐标大
的纵坐标大![]() ,
,
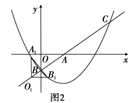
∴![]() ,
,
解得![]() ,
,
综上所述,点![]() 的横坐标为
的横坐标为![]() 或
或![]() .
.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案