题目内容

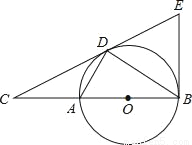
如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．（1）判断直线CD和⊙O的位置关系，并说明理由．

（2）过点B作⊙O的切线BE交直线CD于点E，若AC=2，⊙O的半径是3，求∠BEC的正切值．

（1）直线CD与⊙O的位置关系是相切．理由见解析；（2 ）. 【解析】【试题分析】 （1）证明切线的方法，知道直线与圆的交点，连接半径证垂直半径，即可. （2）BC已知，关键是求BE 的长度，在Rt 中，OA=5，OD=3，根据勾股定理得CD=4，在Rt 中,设BE=DE=x，列出勾股定理方程（4+x）2=x2+（5+3）2，解得：x=6，所以tan∠BEC=. 【试题解析...
练习册系列答案
相关题目

如图，在△ABC中，AC=DC=DB，∠ACD=100°，求∠B的度数．

∠B=20°. 【解析】试题分析：根据等边对等角和三角形的内角和定理，可先求得∠CAD的度数；再根据外角的性质，求∠B的度数． 试题解析：【解析】 ∵AC=DC=DB，∠ACD=100°，∴∠CAD=（180°-100°）÷2=40°，∵∠CDB是△ACD的外角，∴∠CDB=∠A+∠ACD=40°+100°=140°，∵DC=DB，∴∠B=（180°-140°）÷2=20°．

小派同学想给数学老师送张生日贺卡，但他只知道老师的生日在10月，那么他一次猜中老师生日的概率是（　　）

A. B. C. D.

D 【解析】试题解析：∵10月一共31天， ∴他一次猜中老师生日的概率是， 故选D．

如右图，Rt△ABC的面积为20cm2，在AB的同侧，分别以AB，BC，AC为直径作三个半圆，则阴影部分的面积为 ．

20cm2 【解析】 试题分析：根据阴影部分的面积等于以AC、CB为直径的两个半圆的面积加上△ABC的面积再减去以AB为直径的半圆的面积列式并整理，再利用勾股定理解答． 【解析】 由图可知，阴影部分的面积=π（AC）2+π（BC）2+S△ABC﹣π（AB）2， =（AC2+BC2﹣AB2）+S△ABC， 在Rt△ABC中，AC2+BC2=AB2， ∴阴影部分的...

如图，在长方形ABCD中，点E在AB边上，将长方形ABCD沿直线DE折叠，点A恰好落在BC边上的点F处．若AE=5，BF=3，则CF的长为（ ）

A. 9 B. 10 C. 12 D. 15

C 【解析】∵四边形ABCD是长方形， ∴∠B=∠C=∠A=90°，AB=CD， 由折叠的性质可得：EF=AE=5，∠EFD=∠A=90°， 在Rt△BEF中，BE==4，∠BFE+∠BEF=90°， ∴CD=AB=AE+BE=5+4=9， ∵∠EFD=90°，∴∠BFE+∠DFC=90°， ∴∠BEF=∠CFD， ∴△BEF∽△CFD， ∴，...

如图，AB=DC，AC=DB，求证：AB∥CD．

详见解析. 【解析】本题考查的是全等三角形的判定与性质、平行线的判定， 先根据“SSS”证得△ABC≌△DCB，即可得到∠ABC=∠DCB，从而得到AB∥CD． ∵ 在△ABC和△DCB中， ， ∴ △ABC≌△DCB（SSS）． ∴ ∠ABC=∠DCB． ∴ AB∥CD．

将a因式内移的结果为　 　．

﹣ 【解析】由题意得：a<0， 故答案是为﹣ .

计算： ．

【解析】试题分析：将特殊角的三角函数值代入求解． 试题解析： 原式= ＝ ＝

如果m表示向东走m，那么向西走m表示为（　　）

A. m B. m C. m D. m

B 【解析】试题分析：因为m表示向东走m，所以向西走m表示为m，故选：B．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网