题目内容
某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若安排甲队先工作a天,余下的由乙队来完成,则乙队完成余下的任务需要多少天?(用含a的代数式表示)
(3)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若安排甲队先工作a天,余下的由乙队来完成,则乙队完成余下的任务需要多少天?(用含a的代数式表示)
(3)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
考点:分式方程的应用,一元一次不等式的应用
专题:
分析:(1)设乙工程队每天能完成绿化的面积是xm2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列方程求解;
(2)用总工作量减去甲队的工作量,然后除以乙队的工作效率即可求解;
(3)设应安排甲队工作a天,根据绿化总费用不超过8万元,列不等式求解.
(2)用总工作量减去甲队的工作量,然后除以乙队的工作效率即可求解;
(3)设应安排甲队工作a天,根据绿化总费用不超过8万元,列不等式求解.
解答:解:(1)设乙工程队每天能完成绿化的面积是xm2,
根据题意得:
-
=4,
解得:x=50,
经检验,x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2;
(2)
=36-2a;
(3)设应安排甲队工作a天,
根据题意得:0.4a+0.25(36-2a)≤8,
解得:a≥10.
答:至少应安排甲队工作10天.
根据题意得:
| 400 |
| x |
| 400 |
| 2x |
解得:x=50,
经检验,x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2;
(2)
| 1800-100a |
| 50 |
(3)设应安排甲队工作a天,
根据题意得:0.4a+0.25(36-2a)≤8,
解得:a≥10.
答:至少应安排甲队工作10天.
点评:本题考查了分式方程和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
当实数x的取值使得
有意义时,函数y=-4x+1中y的取值范围是( )
| x-3 |
| A、y≥-11 |
| B、y≤-11 |
| C、y≥-13 |
| D、y≤-13 |
已知,一元二次方程a(x+m)2+b=0的两根为1,2,则a(x+m-2)2+b=0的两根为( )
| A、3,4 |
| B、-1,0 |
| C、与a、m、b的值有关 |
| D、无法求出 |
在下列图形中,以O为端点的射线条数一样多的是( )


| A、(1)与(2) |
| B、(2)与(3) |
| C、(1)与(3) |
| D、(1)、(2)与(3) |
 某校组织部分学生到离校路程10千米的“滨江湿地公园”进行综合实践活动,为倡导“低碳出行,绿色生活”的理念,他们先以4千米/小时的速度步行,再以12千米/小时骑公共自行车行完余下的路程,全程共用了70分钟.求步行和骑车各用了多少时间?
某校组织部分学生到离校路程10千米的“滨江湿地公园”进行综合实践活动,为倡导“低碳出行,绿色生活”的理念,他们先以4千米/小时的速度步行,再以12千米/小时骑公共自行车行完余下的路程,全程共用了70分钟.求步行和骑车各用了多少时间?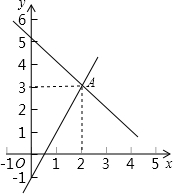 如图,点A的坐标可以看成是方程组
如图,点A的坐标可以看成是方程组