题目内容
 如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段AB上以2cm/s的速度由B向C点运动,同时,点Q在先由CA上由C点向A点运动,若运动时间为t秒.
如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段AB上以2cm/s的速度由B向C点运动,同时,点Q在先由CA上由C点向A点运动,若运动时间为t秒.(1)用含有t的代数式表示CP;
(2)若点Q的运动速度与点P的运动速度相等,经过几秒后,△BPD与△CQP全等;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
考点:全等三角形的判定,等腰三角形的性质
专题:动点型
分析:(1)由题可表示出BP=2t,则CP=BC-BP=10-2t;
(2)BD=6cm,BP=2t,CP=10-2t,CQ=2t,若△BPD与△CPQ全等,则有PC=BD,可求得t;
(3)由∠B=∠C,若△BPD与△CPQ全等,则有BD=PC,或BD=CQ,再利用t表示出线段长度,求出t即可.
(2)BD=6cm,BP=2t,CP=10-2t,CQ=2t,若△BPD与△CPQ全等,则有PC=BD,可求得t;
(3)由∠B=∠C,若△BPD与△CPQ全等,则有BD=PC,或BD=CQ,再利用t表示出线段长度,求出t即可.
解答:解:(1)由题意可知BP=2t,则CP=BC-BP=10-2t;
(2)∵D为AB中点,
∴BD=6cm,BP=2t,CP=10-2t,
当Q点的速度与P点的速度相等时,则有CQ=2t,
此时CQ=BP,且∠B=∠C,
∴当△BPD和△CQP全等时有BD=PC,
即6=10-2t,解得t=2s,
∴若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPD与△CQP全等;
(3)∵AB=AC,
∴∠B=∠C,
∵Q点速度和P点速度不相等,
∴BP≠CQ,
∴当△BPD与△CPQ全等时,有BD=CQ=6cm,BP=CP,
即2t=10-2t,解得t=2.5s,
∴Q点的速度为:
=
=2.4cm/s.
(2)∵D为AB中点,
∴BD=6cm,BP=2t,CP=10-2t,
当Q点的速度与P点的速度相等时,则有CQ=2t,
此时CQ=BP,且∠B=∠C,
∴当△BPD和△CQP全等时有BD=PC,
即6=10-2t,解得t=2s,
∴若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPD与△CQP全等;
(3)∵AB=AC,
∴∠B=∠C,
∵Q点速度和P点速度不相等,
∴BP≠CQ,
∴当△BPD与△CPQ全等时,有BD=CQ=6cm,BP=CP,
即2t=10-2t,解得t=2.5s,
∴Q点的速度为:
| CQ |
| t |
| 6 |
| 2.5 |
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键.注意利用t表示出各线段的长,化动为静是解这类问题的基本思路.

练习册系列答案
相关题目
若(x+5)2与|y-7|值互为相反数,下列代数式的值最大的是( )
| A、x+y | B、x-y |
| C、-x+y | D、-x-y |
某地区2010年投入教育经费2500万元,预计到2012年共投入8000万元.设这两年投入教育经费的年平均增长率为x,则下列方程正确的是( )
| A、2500+2500(1+x)+2500(1+x)2=8000 |
| B、2500x2=8000 |
| C、2500(1+x)2=8000 |
| D、2500(1+x)+2500(1+x)2=8000 |
下列说法正确的是( )
| A、-81的平方根是±9 |
| B、任何一个非负数的平方根都不大于这个数 |
| C、任何数的平方是非负数,因而任何数的平方根也是非负数 |
| D、2是4的平方根 |
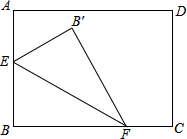 如图,矩形ABCD,AB=3,BC=4,E、F是AB、BC边上的动点,以EF为轴翻折△BEF得△B′EF,连接AB′,求AB′的最小值.
如图,矩形ABCD,AB=3,BC=4,E、F是AB、BC边上的动点,以EF为轴翻折△BEF得△B′EF,连接AB′,求AB′的最小值.