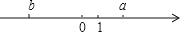题目内容
某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.
(1)如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?
(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.
①租用甲型汽车8辆、乙型汽车12辆;②租用甲型汽车9辆、乙型汽车11辆; ③租用甲型汽车10辆、乙型汽车10辆.(2)最省钱的租车方案是:租用甲型汽车8辆、乙型汽车12辆. 【解析】试题分析:(1)首先根据题意列出不等式组得 解出的取值范围,最后确定的取值,进而确定出具体方案; (2)首先求出关于租车总费用的函数关系式,再根据一次函数的增减性确定总费用最小的租车方案. 试...
练习册系列答案
相关题目


 ,②
,②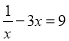 ,③
,③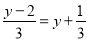 ,④
,④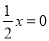 ,是一元一次方程的有________.(填番号)
,是一元一次方程的有________.(填番号)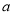 在数轴上对应的点如图所示,则
在数轴上对应的点如图所示,则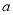 ,
, 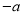 ,1的大小关系正确的是( )
,1的大小关系正确的是( )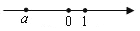
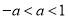 B.
B. 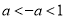 C.
C. 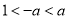 D.
D. 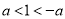
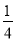 )﹣1﹣|﹣
)﹣1﹣|﹣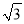 |﹣20110+(
|﹣20110+(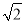 )2+tan60°;
)2+tan60°;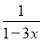 ﹣
﹣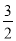 =
=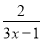 .
.
 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB. ,求AC的长.
,求AC的长.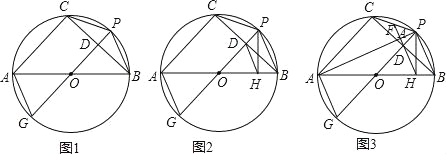
 ,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.
,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.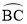 的中点P作⊙O的直径PG,
的中点P作⊙O的直径PG,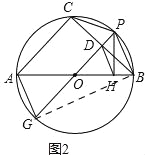
 ,
, (180°﹣∠BOP)=∠OPB,
(180°﹣∠BOP)=∠OPB,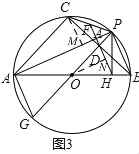
 ∠COP=∠CAP,
∠COP=∠CAP, ,
, ,
, ,
,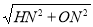 =5,
=5, =10.
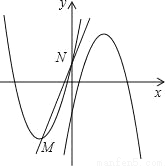
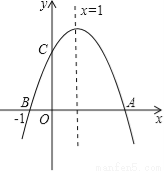
=10. 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点. x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;