Question

如图，AB是⊙O的直径，直线EF切⊙O于点C， AD⊥EF于点D．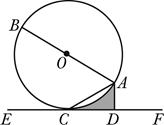

（1）求证：AC平分∠BAD；
（2）若⊙O的半径为2，∠ACD＝30°，求图中阴影部分的面积．（结果保留）

Answer 1

（1）根据角平分线把角平分的性质来求证此角（2）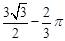

解析试题分析：（1）证明：连接OC
∵直线EF切⊙O 于点C
∴OC⊥EF
∵AD⊥EF
∴OC∥AD                                  2分
∴∠OCA=∠DAC
∵ OA=OC
∴∠BAC=∠OCA                            4分
∴∠DAC=∠BAC
即AC平分∠BAD                            5分
（2）∵∠ACD=30°，∠OCD=90°
∴∠OCA=60°.
∵OC=OA
∴△OAC是等边三角形
∵⊙O的半径为2
∴AC=OA=OC=2，∠AOC=60°                    7分
∵在Rt△ACD中，AD=AC=1
由勾股定理得：DC=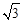                       8分
∴阴影部分的面积=S_梯形OCDA﹣S_扇形OCA
=×（2+1）×﹣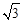
    
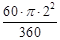
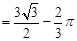
∴阴影部分的面积为：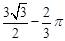      
考点：等边三角形，角平分线
点评：等边三角形的三边相等，且三个内角都是60度，有一个内角是60的等腰三角形也是等边三角形，两个内角都是60度的三角形是等边三角形