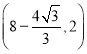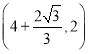题目内容
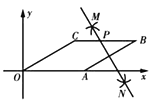
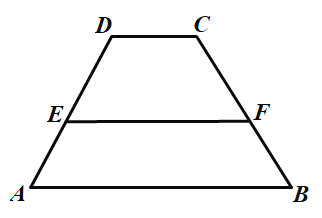
【题目】已知：如图所示，梯形ABCD中，
，点E、F分别在腰AD、BC上，且AB=7，CD=3，AE：DE=BF：CF=2：3，求EF的长．
【答案】
【解析】
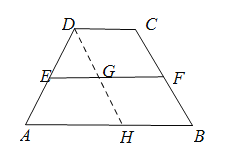
过点D作DH∥CB，交EF于点G，交AB于点H，根据AE：DE=BF：CF，得出
，由此可得四边形DCBH是平行四边形，CD=GF=BH，再根据可得△DEG∽△DAH，即
=
=
，由此即可算出EF．
过点D作DH∥CB，交EF于点G，交AB于点H，
∵AE：DE=BF：CF=2：3，
∴可得，
∵
，DH∥CB，
∴四边形DCBH是平行四边形，
∴CD=GF=BH，
∵，
∴△DEG∽△DAH，
∴==，
∵AB=7，CD=3，
∴AH=4，CD=GF=BH=3，
∴EG=
，
∴EF=EG+GF=+3=
．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
