��Ŀ����
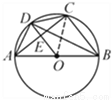
��ͼ,��O �İ뾶Ϊ��,ֱ��CD ����Բ��O,����O ��C��D ����,ֱ��AB��CD,�� M ��ֱ��CD �����ڵ�C��O��D ��һ������,AM ���ڵ�ֱ�߽���O �ڵ�N,�� P ��ֱ��CD ����һ��,��PM��PN��
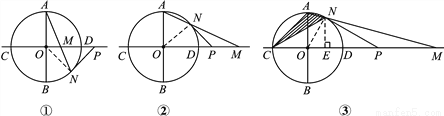
(1)���� M �ڡ�O �ڲ�,��ͼ��,���ж� PN ���O �Ĺ�ϵ,��д��֤������;
(2)���� M �ڡ�O �ⲿ,��ͼ��,������������ʱ,(1)�Ľ����Ƿ���? ��˵������;
(3)���� M �ڡ�O �ⲿ,��ͼ��,��AMO��15��,��ͼ����Ӱ���ֵ������
(1)�����������2�����������������������3�������� �������������������1��PN ���O ���У�Ҫ֤��ONPN���ɣ�����ON��PM��PN�����ԡ�PNM����PMN����AMO����PMN��AB��CD,���ԡ�PMN+��MAO=90�㣬�����MAO=��MNO,���ԡ�PNM+��MNO=90�㣬����PN ���O ���У���2�����������е�����������MAO+��OMA=90�㣬���OMA=��PNM����MAO...
��ϰ��ϵ�д�
�����Ŀ


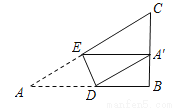
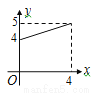 B.
B. 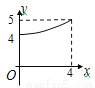
 D.
D.