题目内容
如图,等边△ABC内接于⊙O,P是 AB 上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC= 度,∠BPC= 度;
(2)求证:△ACM≌△BCP;
(3)若PA=3,PB=6,求梯形PBCM的面积.

(1)解:∠APC=60°,∠BPC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°-∠BPM=180°-(∠APC+∠BPC)=180°-120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PBC=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
∴△ACM≌△BCP;
(3)解:作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+PB=3+6=9,
在Rt△PMH中,∠MPH=30°,
∴PH= ,∴S梯形PBCM=
,∴S梯形PBCM= (PB+CM)×PH=
(PB+CM)×PH= (6+9)×
(6+9)× =
= …
…

练习册系列答案
相关题目
 . [根据当涂县模拟试卷改编]
. [根据当涂县模拟试卷改编]

 A. 2月 B. 5月 C. 6月 D. 7月
A. 2月 B. 5月 C. 6月 D. 7月 中,
中, ,
, ,
, .三角板绕直角顶点
.三角板绕直角顶点 逆时针旋转,当点
逆时针旋转,当点 的对应点
的对应点 落在
落在 边的起始位置上时即停止转动,则阴影部分的面积
边的起始位置上时即停止转动,则阴影部分的面积 
 m B.
m B.  m C.
m C.  m D.
m D.  m
m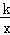 交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k的值为( )
交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k的值为( )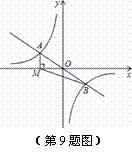
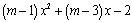 (m为常数,且m¹1)。
(m为常数,且m¹1)。