题目内容
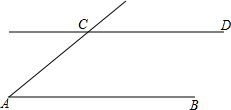 (2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
(2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于| 1 | 2 |
(1)根据题意,利用直尺与圆规,把图补充完整,若∠ACD=114°,求∠MAB的度数;
(2)利用直尺与圆规作CN⊥AM,垂足为N,交AB于Q,求证:四边形AQMC是菱形.
分析:(1)根据题目要求画出图形,再根据平行线的性质可得:∠CAB=180°-114°=66°,再根据角平分线的性质可得:∠MAB=
∠CAB=33°;
(2)首先证明AC=CM,再证明△ACN≌△AQN可得AC=AQ,进而得到CM=AQ,再有CM∥AQ可得四边形AQMC是平行四边形,再有条件AC=CM可证明四边形AQMC是菱形.
| 1 |
| 2 |
(2)首先证明AC=CM,再证明△ACN≌△AQN可得AC=AQ,进而得到CM=AQ,再有CM∥AQ可得四边形AQMC是平行四边形,再有条件AC=CM可证明四边形AQMC是菱形.
解答: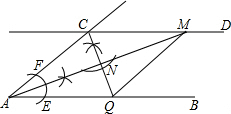 解:(1)把图补充完整(保留痕迹),
解:(1)把图补充完整(保留痕迹),
由AB∥CD,得∠CAB+∠ACD=180°
所以:∠CAB=180°-114°=66°,
由作图,得:AD是∠CAB的平分线,
所以:∠MAB=
∠CAB=33°;
(2)证明:利用直尺与圆规作CN⊥AM,垂足为N(保留痕迹),
∵AB∥CD,
∴∠DAB=∠CDA
又∵AD是∠CAB的平分线,
∴∠DAB=∠CAD,
∴AC=CM,
在△ACN与△AQN中,
,
∴△ACN≌△AQN(ASA),
∴AC=AQ,
∴CM=AC=AQ.
又∵AB∥CD,
∴四边形AQMC是菱形.
 解:(1)把图补充完整(保留痕迹),
解:(1)把图补充完整(保留痕迹),由AB∥CD,得∠CAB+∠ACD=180°
所以:∠CAB=180°-114°=66°,
由作图,得:AD是∠CAB的平分线,
所以:∠MAB=
| 1 |
| 2 |
(2)证明:利用直尺与圆规作CN⊥AM,垂足为N(保留痕迹),
∵AB∥CD,
∴∠DAB=∠CDA
又∵AD是∠CAB的平分线,
∴∠DAB=∠CAD,
∴AC=CM,
在△ACN与△AQN中,
|
∴△ACN≌△AQN(ASA),
∴AC=AQ,
∴CM=AC=AQ.
又∵AB∥CD,
∴四边形AQMC是菱形.
点评:此题主要考查了复杂作图,关键是根据题意正确画出图形,掌握菱形的判定定理.

练习册系列答案
相关题目
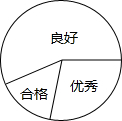 (2013•怀集县二模)九年级(3)班期末考试合格、良好、优秀的比例是1:6:3,小明同学画了一个半径为2cm的圆形的统计图(如图).则表示“良好”的部分的面积是
(2013•怀集县二模)九年级(3)班期末考试合格、良好、优秀的比例是1:6:3,小明同学画了一个半径为2cm的圆形的统计图(如图).则表示“良好”的部分的面积是 (2013•怀集县二模)如图,已知反比例函数
(2013•怀集县二模)如图,已知反比例函数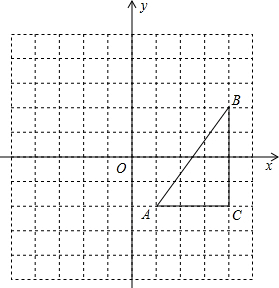
 (2013•怀集县二模)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(2013•怀集县二模)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.