题目内容
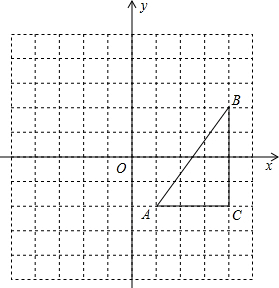
(2013•怀集县二模)(1)根据两点坐标,构造直角三角形,求出两直角边的长,然后再求斜边的长.
(2)观察表格中的关系,探究任意两点坐标P1(x1,y1),P2(x2,y2)与P1、P2之间的距离P1P2有什么关系?并证明你的结论.
(3)求函数y=
+
的最小值.
| 两点坐标 | 构造 直角三角形 |
一直角边长 | 另一直角 边长 |
斜边长 | ||||||||
| A(1,-2) B(4,2) |
RT△ABC | AC=4-1=3 | BC=2-(-2) | AB=
| ||||||||
| M(-4,2) N(1,-3) |
RT△ MPN MPN |
PN=1-(-4)=5 PN=1-(-4)=5 |
PM=2-(-3)=5 PM=2-(-3)=5 |
MN=
|
(3)求函数y=
| (x-1)2+4 |
| (x-4)2+4 |

分析:(1)利用点的坐标得出线段长度即可;
(2)利用已知得出P1P=x2-x1,P2P=y2-y1,进而利用勾股定理得出公式即可;
(3)设x轴上有点P,利用点之间距离公式进而得出答案.
(2)利用已知得出P1P=x2-x1,P2P=y2-y1,进而利用勾股定理得出公式即可;
(3)设x轴上有点P,利用点之间距离公式进而得出答案.
解答:解:(1)如图所示:
(2)P1P2=
;
 证明:构造直角三角形P1P2P,∠P=90°,
证明:构造直角三角形P1P2P,∠P=90°,
则P1P=x2-x1,P2P=y2-y1,
根据勾股定理,得P1P2=
;
(3)设x轴上有点P
因为y=
+
=
+
=PA+PB≥AB
=
=5,
所以函数y=
+
的最小值是5.
| 两点坐标 | 构造 直角三角形 |
一直角边长 | 另一直角 边长 |
斜边长 | ||||
| A(1,-2) B(4,2) |
RT△ABC | AC=4-1=3 | BC=2-(-2) | AB=
| ||||
| M(-4,2) N(1,-3) |
RT△MPN | PN=1-(-4)=5 | PM=2-(-3)=5 | MN=
|
| (x1-x2)2+(y2-y1)2 |
 证明:构造直角三角形P1P2P,∠P=90°,
证明:构造直角三角形P1P2P,∠P=90°,则P1P=x2-x1,P2P=y2-y1,
根据勾股定理,得P1P2=
| (x1-x2)2+(y2-y1)2 |
(3)设x轴上有点P
因为y=
| (x-1)2+4 |
| (x-4)2+4 |
| (x-1)2+[0-(-2)]2 |
| (x-4)2+(0-2)2 |
=
| (4-1)2+[2-(-2)]2 |
所以函数y=
| (x-1)2+4 |
| (x-4)2+4 |
点评:此题主要考查了坐标图形的性质以及两点之间的距离公式,利用数形结合得出是解题关键.

练习册系列答案
相关题目
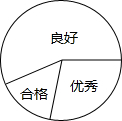 (2013•怀集县二模)九年级(3)班期末考试合格、良好、优秀的比例是1:6:3,小明同学画了一个半径为2cm的圆形的统计图(如图).则表示“良好”的部分的面积是
(2013•怀集县二模)九年级(3)班期末考试合格、良好、优秀的比例是1:6:3,小明同学画了一个半径为2cm的圆形的统计图(如图).则表示“良好”的部分的面积是 (2013•怀集县二模)如图,已知反比例函数
(2013•怀集县二模)如图,已知反比例函数 (2013•怀集县二模)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(2013•怀集县二模)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.