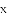题目内容
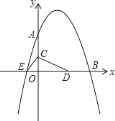
如图,已知抛物线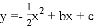 与坐标轴分别交于点
与坐标轴分别交于点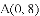
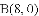
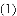
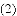
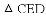
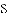


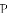
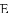
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
八年级一班要在赵研、钱进、孙兰、李丁四名同学中挑选一名同学去参加数学竞赛,四名同学在5次数学测试中成绩的平均数x及方差S2如下表所示:
甲 | 乙 | 丙 | 丁 | |
| 85 | 93 | 93 | 86 |
S2 | 3 | 3 | 3.5 | 3.7 |
如果选出一名成绩较好且状态稳定的同学去参赛,那么应选( )
A. 赵研 B. 钱进 C. 孙兰 D. 李丁


 度数是( )
度数是( )
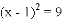 ;
; 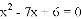 ;
; 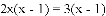



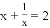 的解为
的解为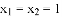 ;
;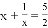 的解为
的解为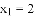 ,
,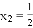 ;
;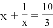 的解为
的解为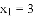 ,
,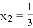 ;
;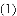
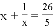 的解为________;
的解为________;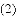
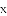
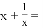 ________的解为
________的解为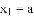 ,
,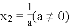 ;
;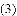
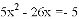 .
.