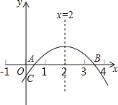题目内容
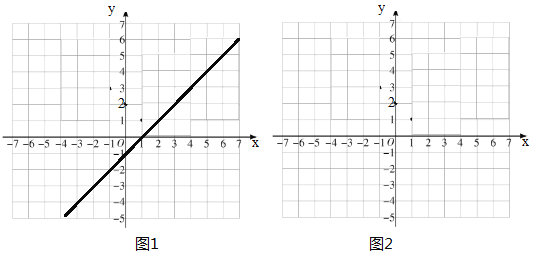
【题目】(1)如图1,结合函数![]() 的图象填空:
的图象填空:![]() 随
随![]() 的增大而___________,当
的增大而___________,当![]() 时,该函数的最大值为_________,最小值为_________.
时,该函数的最大值为_________,最小值为_________.
(2)根据学习函数的经验来探究函数![]() 的最小值.
的最小值.
①若点![]() 和点
和点![]() 是该函数图象上的两点,则
是该函数图象上的两点,则![]() _________;
_________;
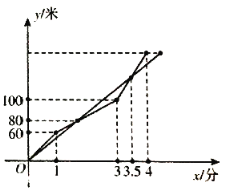
②在平面直角坐标系中描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;
③由图象可知,函数![]() 的最小值为___________.
的最小值为___________.
(3)请结合![]() 的取值范围判断方程
的取值范围判断方程![]() 的解的个数.(直接写出结果)
的解的个数.(直接写出结果)
【答案】(1)增大,2,![]() ;(2)①2;②详见解析;③1;(3)当
;(2)①2;②详见解析;③1;(3)当![]() 时,原方程无解,当
时,原方程无解,当![]() 时,原方程有1个解,当
时,原方程有1个解,当![]() 时,原方程有两个不相等的解(或有两个解).
时,原方程有两个不相等的解(或有两个解).
【解析】
(1)根据一次函数的性质及函数图象上点的坐标特征即可得到答案;
(2)①去掉绝对值符号得到函数的解析式为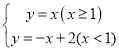 ,把点
,把点![]() 和点
和点![]() 的坐标分别代入计算即可求得答案;
的坐标分别代入计算即可求得答案;
②通过列表、描点、连线即可画出该函数的图象;
③观察函数的图象即可获得答案;
(3)当![]() 、
、![]() 、
、![]() 时,分别讨论方程
时,分别讨论方程![]() 的解的个数即可.
的解的个数即可.
(1)观察函数![]() 的图象,
的图象,![]() 随
随![]() 的增大而增大,
的增大而增大,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴当![]() 时,该函数的最大值为2,最小值为-2,
时,该函数的最大值为2,最小值为-2,
故答案为:增大,2,![]() ;
;
(2)①函数![]() 的解析式为
的解析式为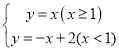 ,
,
∵点![]() 和点
和点![]() 纵坐标相等,
纵坐标相等,
∴点![]() 和点
和点![]() 分别在两个函数的图象上,
分别在两个函数的图象上,
不妨设点![]() 在
在![]() 的图象上,则点
的图象上,则点![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,
,![]() ,
,
即![]() ,
,
解得:![]() ,
,
故答案为:![]() ;
;
② 列表得:
|
| -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|
|
| 4 | 3 | 2 | 1 | 2 | 3 | 4 |
|
描点、连线,如图所示:
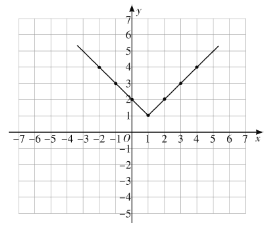
③观察函数的图象可知:当![]() 时,函数取得最小值为: 1,
时,函数取得最小值为: 1,
故答案为:1;
(3)观察函数的图象,
当![]() 时,原方程无解,
时,原方程无解,
当![]() 时,原方程有1个解,
时,原方程有1个解,
当![]() 时,原方程有两个不相等的解.
时,原方程有两个不相等的解.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目