Question

【题目】如图，△ABC中， D、E是AB上的两点，△CDE是等边三角形.

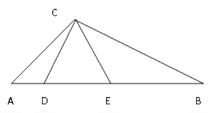
求证：（1）△ABC∽△ACD；

（2）△ACD∽△CBE；

（3）.

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）见解析.

【解析】

（1）找到公共角∠A，再genju 等量代换得到∠ADC=120°=∠ACB，即可证明相似.

（2）由（1）得到∠ACD=∠B，再可得∠ADC=120°=∠CEB，即可证明相似.

（3）由（2）得△ACD∽△CEB，则 ，由CD=CE=DE，等量代换即可证明.

（1）∵△CDE是等边三角形

∴∠CDE=60°

∴∠ADC=120°=∠ACB

又∵∠A=∠A

∴△ABC∽△ACD

（2）∵△CDE是等边三角形

∴∠CDE=60°=∠CED CD=CE=DE

∴ ∠ADC=120°=∠CEB

又∵△ABC∽△ACD

∴∠ACD=∠B

∴△ACD∽△CEB

（3） ∵△ACD∽△CEB

∴

又∵ CD=CE=DE

∴

∴