题目内容
5.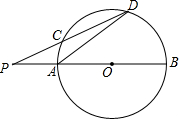 如图,PAB、PCD是⊙O的两条割线,且PAB经过圆心O,若$\widehat{DB}$=$\widehat{DC}$,∠P=24°,则∠ADC=14°.
如图,PAB、PCD是⊙O的两条割线,且PAB经过圆心O,若$\widehat{DB}$=$\widehat{DC}$,∠P=24°,则∠ADC=14°.
分析 连接:BD,由AB为⊙O的直径,得到∠DAB+∠B=90°,根据外角的性质得到∠DAB=∠P+∠ADC=24°+∠ADC,由于$\widehat{DB}$=$\widehat{DC}$,于是得到∠B=∠DAC+∠ADC,于是得到∠DAB+∠B=2(24°+∠ADC)+∠ADC=90°,即可得到结果.
解答 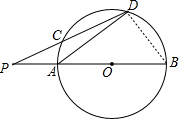 解:连接:BD,
解:连接:BD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠B=90°,
∵∠DAB=∠P+∠ADC=24°+∠ADC,
∵$\widehat{DB}$=$\widehat{DC}$,
∴∠B=∠DAC+∠ADC,
∴∠DAB+∠B=2(24°+∠ADC)+∠ADC=90°,
∴∠ADC=14°,
故答案为:14°.
点评 本题考查了圆周角定理,三角形外角的性质,直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
15. 如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )
如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )
 如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )
如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )| A. | 13个 | B. | 14个 | C. | 15个 | D. | 16个 |
20.抛物线y=(x-2)(x+6)与y轴的交点坐标是( )
| A. | (0,-2) | B. | (0,6) | C. | (0,-12) | D. | (0,12) |
15. 某班同学对某市市民对于2012年伦敦奥运会这件事的了解程度进行调查,他们将了解程度分为“清楚”、“了解”、“知道”、“不知道”四级,将调查结果绘制成以下统计表和条形统计图
某班同学对某市市民对于2012年伦敦奥运会这件事的了解程度进行调查,他们将了解程度分为“清楚”、“了解”、“知道”、“不知道”四级,将调查结果绘制成以下统计表和条形统计图
(1)这次调查的样本容量是200人;
(2)若将四种情况用扇形统计图表示,则“了解”和“知道”两种情况所对和圆心角和为306度;
(3)补充统计表和条形统计图;
(4)若某市共有市民480万人,请你估计“清楚”这一事件的可能有多少人?
 某班同学对某市市民对于2012年伦敦奥运会这件事的了解程度进行调查,他们将了解程度分为“清楚”、“了解”、“知道”、“不知道”四级,将调查结果绘制成以下统计表和条形统计图
某班同学对某市市民对于2012年伦敦奥运会这件事的了解程度进行调查,他们将了解程度分为“清楚”、“了解”、“知道”、“不知道”四级,将调查结果绘制成以下统计表和条形统计图 | 了解程度 | 清楚 | 了解 | 知道 | 不知道 |
| 频数 | 25 | 90 | 80 | 5 |
| 频率 | 0.125 | 0.45 | 0.4 | 0.025 |
(2)若将四种情况用扇形统计图表示,则“了解”和“知道”两种情况所对和圆心角和为306度;
(3)补充统计表和条形统计图;
(4)若某市共有市民480万人,请你估计“清楚”这一事件的可能有多少人?
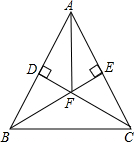 如图,已知,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC与点E,BE、CD相交于点F,连结AF.求证:∠BAF=∠CAF.
如图,已知,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC与点E,BE、CD相交于点F,连结AF.求证:∠BAF=∠CAF.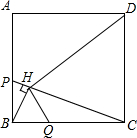 如图,P、Q是正方形ABCD边AB、BC上的点,BH⊥PC,垂足为H,且DH⊥HQ.
如图,P、Q是正方形ABCD边AB、BC上的点,BH⊥PC,垂足为H,且DH⊥HQ.