题目内容
12.一圆锥的侧面展开后是扇形,该扇形的圆心角为120°,半径为6cm,则此圆锥的底面圆的面积为4πcm2.分析 设圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=$\frac{120•π•6}{180}$,然后求出r后利用圆的面积公式求解.
解答 解:设圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{120•π•6}{180}$,解得r=2,
所以圆锥的底面圆的面积=π•22=4π(cm2).
故答案为4π.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
17.下列命题中,是真命题的是( )
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 依次连接四边形四边中点所组成的图形是矩形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
4.下列运算中正确的是( )
| A. | a3•a2=a6 | B. | (a3)4=a7 | C. | a5+a5=2a5 | D. | a6÷a3=a2 |
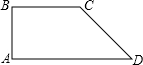 已知直角梯形上底3cm,下底5cm,另一个底角为45°,建立适当直角坐标系并写出图形中的四个顶点的坐标,求出梯形的面积.
已知直角梯形上底3cm,下底5cm,另一个底角为45°,建立适当直角坐标系并写出图形中的四个顶点的坐标,求出梯形的面积.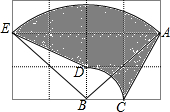 如图所示,格点△ABC绕点B逆时针旋转得到△EBD,图中每个小正方形的边长是1,则图中阴影部分的面积为$\frac{7π}{4}$.
如图所示,格点△ABC绕点B逆时针旋转得到△EBD,图中每个小正方形的边长是1,则图中阴影部分的面积为$\frac{7π}{4}$.