题目内容
如图,二次函数y=
x2+c的图象经过点D(-
,
),与x轴交于A,B两点.
(1)求c的值;
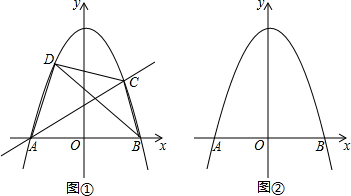
(2)如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;
(3)设点P,Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P,Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由(图②供选用).
| 1 |
| 2 |
| 3 |
| 9 |
| 2 |
(1)求c的值;
(2)如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;
(3)设点P,Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P,Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由(图②供选用).

考点:二次函数综合题
专题:
分析:(1)将D点坐标代入抛物线的解析式中,即可求出待定系数c的值;
(2)若△ACD与△ABC的面积相等,则两个三角形中,AC边上的高相等,设AC、BD的交点为E,若以CE为底,AC边上的高为高,可证得△CED和△CEB的面积相等;这两个三角形中,若以DE、BE为底,则两个三角形同高,那么DE=BE,由此可证得AC平分BD;
由于E是BD的中点,根据B、D的坐标,即可求出E点的坐标,根据A、E的坐标即可用待定系数法求出直线AC的解析式;
(3)设抛物线顶点为N(0,6),在Rt△AON中,易得AN=4
,于是以A点为圆心,AB=4
为半径作圆与抛物线在x轴上方一定有交点Q,连接AQ,再作∠QAB平分线AP交抛物线于P,连接BP,PQ,此时由“边角边”易得△AQP≌△ABP.
(2)若△ACD与△ABC的面积相等,则两个三角形中,AC边上的高相等,设AC、BD的交点为E,若以CE为底,AC边上的高为高,可证得△CED和△CEB的面积相等;这两个三角形中,若以DE、BE为底,则两个三角形同高,那么DE=BE,由此可证得AC平分BD;
由于E是BD的中点,根据B、D的坐标,即可求出E点的坐标,根据A、E的坐标即可用待定系数法求出直线AC的解析式;
(3)设抛物线顶点为N(0,6),在Rt△AON中,易得AN=4
| 3 |
| 3 |
解答:解:(1)将点D代入二次函数y=
x2+c中,
则有
=
+c,
∴c=6;
(2)作CF⊥BD,AG⊥BD,

∵直线AC将四边形ABCD的面积二等分,
∴S△ACD=S△ACB,
∵S△ACD=S△CDE+S△ADE,S△ACB=S△BCF+S△ABF,
∴S△CDE+S△ADE=S△BCF+S△ABF,
∴
DE•AG+
DE•CF=
BE•AG+
BE•CF,即
DE(AG+CF)=
BE(AG+CF),
∴BE=DE,即线段BD被直线AC平分,
∵二次函数解析式为y=
x2+6,A,C为抛物线与x轴交点,
∴C点坐标为(2
,0),A点坐标为(-2
,0),
∵E是BD中点,
∴E点坐标为(
,
)
∴直线AC经过A,E两点,
设直线AC解析式为y=kx+b,则有
,
解得:b=
,k=
,
∴直线AC解析式为y=
x+
;
(3)存在.

设抛物线顶点为N(0,6),
在Rt△AON中,易得AN=4
,
于是以A点为圆心,AB=4
为半径作圆与抛物线在x轴上方一定有交点Q,连接AQ,
再作∠QAB平分线AP交抛物线于P,连接BP,PQ,
此时由“边角边”易得△AQP≌△ABP.
| 1 |
| 2 |
则有
| 9 |
| 2 |
| 3 |
| 2 |
∴c=6;
(2)作CF⊥BD,AG⊥BD,

∵直线AC将四边形ABCD的面积二等分,
∴S△ACD=S△ACB,
∵S△ACD=S△CDE+S△ADE,S△ACB=S△BCF+S△ABF,
∴S△CDE+S△ADE=S△BCF+S△ABF,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=DE,即线段BD被直线AC平分,
∵二次函数解析式为y=
| 1 |
| 2 |
∴C点坐标为(2
| 3 |
| 3 |
∵E是BD中点,
∴E点坐标为(
| ||
| 2 |
| 9 |
| 4 |
∴直线AC经过A,E两点,
设直线AC解析式为y=kx+b,则有
|
解得:b=
| 9 |
| 5 |
3
| ||
| 10 |
∴直线AC解析式为y=
3
| ||
| 10 |
| 9 |
| 5 |
(3)存在.

设抛物线顶点为N(0,6),
在Rt△AON中,易得AN=4
| 3 |
于是以A点为圆心,AB=4
| 3 |
再作∠QAB平分线AP交抛物线于P,连接BP,PQ,
此时由“边角边”易得△AQP≌△ABP.
点评:此题主要考查了一次函数与二次函数解析式的确定、三角形面积的求法、以及全等三角形和直角三角形的判定和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
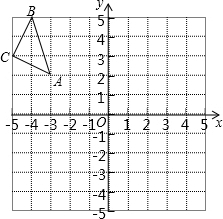 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).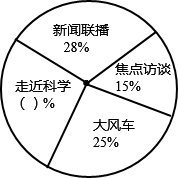 如图是某学校教师喜欢看的电视节目统计图.
如图是某学校教师喜欢看的电视节目统计图.