Question

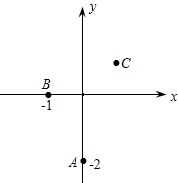已知二次函数过点A（0，-2），B（-1，0），C（

5

4

，

9

8

）
（1）求此二次函数的解析式；
（2）判断点M（1，

1

2

）是否在直线AC上；
（3）过点M（1，

1

2

）作一条直线l与二次函数的图象交于E、F两点（不同于A，B，C三点），请自已给出E点的坐标，并证明△BEF是直角三角形．

Answer 1

分析：（1）已知二次函数过点A（0，-2），B（-1，0），C（

5

4

，

9

8

），欲求解析式，只需用待定系数法进行求解．
（2）由（1）中A、C坐标，通过待定系数法可求出直线AC解析式，把M坐标代入解析式里，看解答结果是否等于

1

2

，若是，则M在AC上，反之不在．
（3）首先E点坐标应符合抛物线，然后可根据待定系数法求出直线EM的解析式，结合二次函数解析式组成方程组，进而求出F点坐标．要想证明△BEF是直角三角形，则必须符合两边的平方和等于第三边的平方，这就需要我们依次求出BE、BF、EF或者是它们的平方进行判定．

解答：解：（1）设二次函数的解析式为y=ax²+bx+c（a≠0），
把A（0，-2），B（-1，0），C（

5

4

，

9

8

）代入
得

c=-2 0=a-b+c 9 8 = 25 16 a+ 5 4 b+c

解得a=2，b=0，c=-2，
∴y=2x²-2（3分）；

（2）设直线AC的解析式为y=kx+b（k≠0），
把A（0，-2），C（

5

4

，

9

8

）代入得

b=-2 9 8 = 5 4 k+b

，
解得k=

5

2

，b=-2，
∴y=

5

2

x-2
当x=1时，y=

5

2

×1-2=

1

2

∴M（1，

1

2

）在直线AC上（5分）；

（3）设E点坐标为（-

1

2

，-

3

2

），则直线EM的解析式为y=

4

3

x-

5

6

由

y= 4 3 x- 5 6 y=2x2-2

化简得2x2-

4

3

x-

7

6

=0，
即(x+

1

2

)(2x-

7

3

)=0，
∴F点的坐标为（

7

6

，

13

18

）．（6分）
过E点作EH⊥x轴于H，则H的坐标为（-

1

2

，0）．
∴EH=

3

2

，BH=

1

2

∴BE²=（

3

2

）²+（

1

2

）²=

10

4

，
同理可得：BF2=(

13

18

)2+(

13

6

)2=

1690

324

=

845

162

，
EF2=(

40

18

)2+(

10

6

)2=

2500

324

=

1250

162

，（9分）
∴BE²+BF²=

10

4

+

845

162

=

1250

162

=EF2，
∴△BEF是直角三角形．（10分）

点评：此题主要考查了待定系数法以及勾股定理逆定理的应用，难易程度适中．