题目内容
 已知二次函数过点A(0,-2),B(-1,0),C(
已知二次函数过点A(0,-2),B(-1,0),C(| 5 |
| 4 |
| 9 |
| 8 |
(1)求此二次函数的解析式;
(2)判断点M(1,
| 1 |
| 2 |
分析:(1)已知二次函数过点A(0,-2),B(-1,0),C(
,
),设二次函数的解析式为y=ax2+bx+c求解析式,用待定系数法进行求解.
(2)由(1)中A、C坐标,设直线AC的解析式为y=kx+b(k≠0),通过待定系数法可求出直线AC解析式,把M横坐标代入解析式里,看解答结果是否等于
,若是,则M在AC上,反之不在.
| 5 |
| 4 |
| 9 |
| 8 |
(2)由(1)中A、C坐标,设直线AC的解析式为y=kx+b(k≠0),通过待定系数法可求出直线AC解析式,把M横坐标代入解析式里,看解答结果是否等于
| 1 |
| 2 |
解答:解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0),
把A(0,-2),B(-1,0),C(
,
)代入
得
,
解得a=2,b=0,c=-2,
∴y=2x2-2;
(2)设直线AC的解析式为y=kx+b(k≠0),
把A(0,-2),C(
,
)代入得
解得k=
,b=-2,
∴y=
x-2
当x=1时,y=
×1-2=
,
∴M(1,
)在直线AC上.
把A(0,-2),B(-1,0),C(
| 5 |
| 4 |
| 9 |
| 8 |
得
|
解得a=2,b=0,c=-2,
∴y=2x2-2;
(2)设直线AC的解析式为y=kx+b(k≠0),
把A(0,-2),C(
| 5 |
| 4 |
| 9 |
| 8 |
|
解得k=
| 5 |
| 2 |
∴y=
| 5 |
| 2 |
当x=1时,y=
| 5 |
| 2 |
| 1 |
| 2 |
∴M(1,
| 1 |
| 2 |
点评:此题主要考查了待定系数法求函数解析式.

练习册系列答案
相关题目
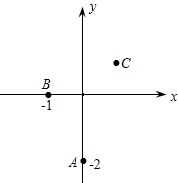 已知二次函数过点A(0,-2),B(-1,0),C(
已知二次函数过点A(0,-2),B(-1,0),C(
 )
) )是否在直线AC上;
)是否在直线AC上; )作一条直线l与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.
)作一条直线l与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.