题目内容
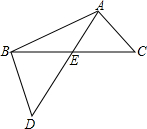 如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使
如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B,D的对应点为A,C,那么线段CE的长应等于
考点:相似三角形的判定
专题:计算题
分析:根据对顶角相等得到∠AEC=∠BED,则根据两组对应边的比相等且夹角对应相等的两个三角形相似,当
=
时,△BDE∽△ACE,然后利用比例性质计算CE的长.
| BE |
| AE |
| DE |
| CE |
解答:解:∵∠AEC=∠BED,
∴当
=
时,△BDE∽△ACE,
即
=
,
∴CE=
.
故答案为
.
∴当
| BE |
| AE |
| DE |
| CE |
即
| 4 |
| 3 |
| 5 |
| CE |
∴CE=
| 15 |
| 4 |
故答案为
| 15 |
| 4 |
点评:本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似,此判定方法要合理使用公共角或对顶角.

练习册系列答案
相关题目
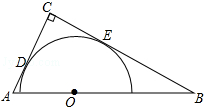 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( )
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( )| A、1 | B、1.5 |
| C、1.6 | D、2.5 |
点P(4,-3)关于原点的对称点是( )
| A、(4,3) |
| B、(-3,4) |
| C、(-4,3) |
| D、(3,-4) |
世界文化遗产长城总长约为6700000米,将6700000用科学记数法可表示为( )
| A、6.7×105 |
| B、6.7×106 |
| C、67×105 |
| D、0.67×107 |
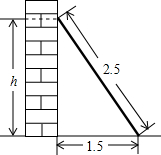 如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h. 如图,△ABC的三个顶点都在格点上,A点的坐标为(-4,2),B点的坐标为(-2,1),C点的坐标为(-1,3)
如图,△ABC的三个顶点都在格点上,A点的坐标为(-4,2),B点的坐标为(-2,1),C点的坐标为(-1,3)