题目内容
 抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).
抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).(1)求该抛物线的解析式及顶点M的坐标;
(2)求△BCM的面积与△ABC的面积的比.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:
分析:(1)由抛物线与x轴交于点A(-1,0),B(3,0)两点,则可设抛物线解析式为y=a(x+1)(x-3).由与y轴交于点C(0,-3),则代入易得解析式,顶点易知.
(2)求△BCM面积与△ABC面积的比,由两三角形不为同高或同底,所以考虑求解求出两三角形面积再作比即可.因为S△BCM=S梯形OCMD+S△BMD-S△BOC,S△ABC=
•AB•OC,则结论易得.
(2)求△BCM面积与△ABC面积的比,由两三角形不为同高或同底,所以考虑求解求出两三角形面积再作比即可.因为S△BCM=S梯形OCMD+S△BMD-S△BOC,S△ABC=
| 1 |
| 2 |
解答:解:(1)设抛物线解析式为y=a(x+1)(x-3),
∵抛物线过点(0,-3),
∴-3=a(0+1)(0-3),
∴a=1,
∴抛物线解析式为y=(x+1)(x-3)=x2-2x-3,
 ∵y=x2-2x-3=(x-1)2-4,
∵y=x2-2x-3=(x-1)2-4,
∴M(1,-4).
(2)如图1,连接BC、BM、CM,作MD⊥x轴于D,
∵S△BCM=S梯形OCMD+S△BMD-S△BOC
=
×(3+4)×1+
×2×4-
×3×3
=
+
-
=3
S△ABC=
•AB•OC=
×4×3=6,
∴S△BCM:S△ABC=3:6=1:2.
∵抛物线过点(0,-3),
∴-3=a(0+1)(0-3),
∴a=1,
∴抛物线解析式为y=(x+1)(x-3)=x2-2x-3,
 ∵y=x2-2x-3=(x-1)2-4,
∵y=x2-2x-3=(x-1)2-4,∴M(1,-4).
(2)如图1,连接BC、BM、CM,作MD⊥x轴于D,
∵S△BCM=S梯形OCMD+S△BMD-S△BOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 7 |
| 2 |
| 8 |
| 2 |
| 9 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BCM:S△ABC=3:6=1:2.
点评:本题考查了待定系数法求解析式、二次函数图象与性质及坐标系中求不规则图形面积等基础考点,难度适中,适合学生练习.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
过多边形的一个顶点可以引出6条对角线,则多边形的边数是( )
| A、7 | B、8 | C、9 | D、10 |
 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,DE⊥AB于点E,AD=4,求BE的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,DE⊥AB于点E,AD=4,求BE的长.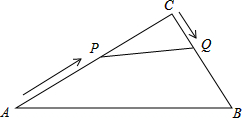 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求: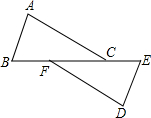 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,AB=DE.求证:FB=CE.
如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,AB=DE.求证:FB=CE.