Question

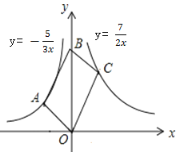
【题目】如图，平行四边形OABC的顶点O，B在y轴上，顶点A在反比例函数y=上，顶点C在反比例函数y=上，则平行四边形OABC的面积是____________．

Answer 1

【答案】

【解析】

先过点A作AE⊥y轴于点E，过点C作CD⊥y轴于点D，再根据反比例函数系数k的几何意义，求得△ABE的面积=△COD的面积相等= ，△AOE的面积=△CBD的面积相等= ，最后计算平行四边形OABC的面积．

解：过点A作AE⊥y轴于点E，过点C作CD⊥y轴于点D，
根据∠AEB=∠CD0=90°，∠ABE=∠COD，AB=CO可得：△ABE≌△COD（AAS），
∴△ABE与△COD的面积相等，
又∵点C在的图象上，
∴△ABE的面积=△COD的面积相等=，
同理可得：△AOE的面积=△CBD的面积相等=，
∴平行四边形OABC的面积=2（+）=+=，