题目内容
3.水果批发商店今年6月份从海南购进了一批高档热带水果,预计6月份(30天)进行试销,购进价格为20元/千克,已知第一天销售量为78千克,后面每增加1天(销售量就减少2千克),据统计,每天销售价格p(元)与销售时间x(天)满足p=x+20(1≤x≤30,且x为整数).(1)求该批发商6月份第几天销售量开始低于56千克?
(2)7月份来临,该热带水果大量上市,受此影响,进价比6月份的进价每千克减少25%,但该批发商加强宣传力度,结果7月份第一天销售量比6月份最后一天的销售量增加了m%,但价格比6月份最后一天的销售价格减少0.4m%,结果7月份第一天的利润达到726元,求m的值(其中1<m<50).
分析 (1)设第n天销售量开始低于56千克,根据第一天销售量为78千克,后面每增加1天(销售量就减少2千克),列不等式求解即可;
(2)根据“销售量×单千克利润=总利润”列方程即可解答.
解答 解:(1)设第n天销售量开始低于56千克,根据题意列不等式得,
78-2(n-1)<56,
解得:n>12,
答:该批发商6月份第13天销售量开始低于56千克.
(2)根据题意列方程,
20(1-m%)•[50(1-0.4m%)-15]=726,
整理得:m2-75m+650=0,
解得:m1=10,m2=65(不合题意舍去)
∴m=10.
点评 本题主要考查了一元一次不等式和一元二次方程的实际应用,正确理解题意,根据题目中的数量关系列出不等式或方程是解决问题的关键.

练习册系列答案
相关题目
12.某书店要经营一种新上市的中考数学复习资料,进价为每本20元,试营销阶段发现每天销售量y(本)与单价x元/本之间满足下表:
(1)观察并分析表中的y与x之间的对应关系,用学过的函数的有关知识写出y(本)与x(元/本)的函数解析式;
(2)写出书店销售这种中考数学复习资料,每天所得的销售利润w(元)与销售单价x(元/本)之间的函数关系式(每天销售利润=每本资料的利润×每天的销售量),并求销售单位为多少时,该书店每天的销售利润最大?最大利润是多少?
(3)书店的销售部结合上述情况,提出了A、B两种营销方案:
方案A:该中考数学复习资料的单价高于进价且不超过26元;
方案B:每天销售量不少于50件,且每本资料的利润至少为18元.
请比较哪种方案的最大利润更高,并说明理由.
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
(2)写出书店销售这种中考数学复习资料,每天所得的销售利润w(元)与销售单价x(元/本)之间的函数关系式(每天销售利润=每本资料的利润×每天的销售量),并求销售单位为多少时,该书店每天的销售利润最大?最大利润是多少?
(3)书店的销售部结合上述情况,提出了A、B两种营销方案:
方案A:该中考数学复习资料的单价高于进价且不超过26元;
方案B:每天销售量不少于50件,且每本资料的利润至少为18元.
请比较哪种方案的最大利润更高,并说明理由.
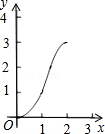
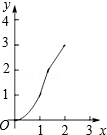
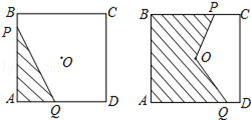 如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )
如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为y cm2,那么y与x的函数关系图象可能是( )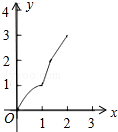
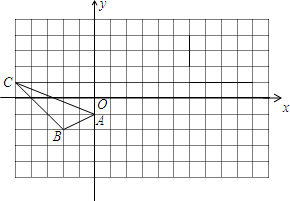 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).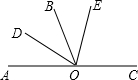 如图所示,若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOA=30°,则∠COE的度数是80°.
如图所示,若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOA=30°,则∠COE的度数是80°.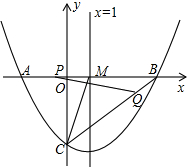 如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.