题目内容
5.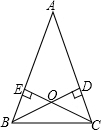 如图,在△ABC中,AB=AC,高BD、CE相交于点O,OB与OC相等吗?请说明理由.
如图,在△ABC中,AB=AC,高BD、CE相交于点O,OB与OC相等吗?请说明理由.
分析 首先根据等腰三角形的性质得到∠ABC=∠ACB,然后利用高线的定义得到∠ECB=∠DBC,从而得证.
解答 证明:∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BEC=∠CDB=90°,BC=CB,
在△BEC与△CDB中,
$\left\{\begin{array}{l}{∠ABC=∠ACB}\\{∠BEC=∠CDB=90°}\\{BC=CB}\end{array}\right.$,
∴△BEC≌△CDB (AAS),
∴∠DBC=∠ECB,
∴OB=OC.
点评 本题考查了等腰三角形的性质和判定的应用,关键是根据AAS证明三角形全等和判定解答.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
20.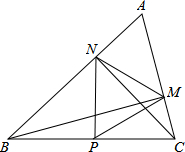 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )
 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )| A. | ①正确 | B. | ②正确 | C. | ①②都正确 | D. | ①②都不正确 |
14.为了从甲乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下两个统计图表:
(1)请补全上述图表;
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?请说明你的理由.

| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 7 | 2.8 | 0 |
| 乙 | 7 | 7.5 | 5.4 | 1 |
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?请说明你的理由.

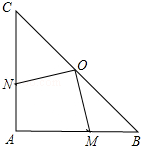 如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.
如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.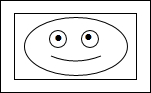 学生会举办摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶上一圈等宽的彩纸(如图).经试验彩纸面积为相片面积的$\frac{17}{27}$时较美观,则镶在彩纸条的宽为2.
学生会举办摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶上一圈等宽的彩纸(如图).经试验彩纸面积为相片面积的$\frac{17}{27}$时较美观,则镶在彩纸条的宽为2. 如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D.
如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D.