Question

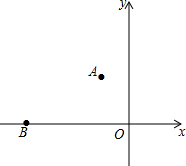如图所示，某警察在点A（-2，4）接到任务，前去阻截在点B（-10，0）的劫包摩托车，劫包摩托车从点B沿x轴向原点方向匀速行驶，警察立即拦下一辆摩托车前去阻截，若两辆摩托车行驶速度相等，则相遇时警察的坐标为

 

．

Answer 1

考点：勾股定理的应用

专题：

分析：根据题意得出AC=BC，再利用勾股定理得出BC的长，即可得出C点坐标．

解答：解：如图所示：过点A作AD⊥x轴于点D，
由题意可得，AC=BC，
则AD=4，BD=6，
设AC=BC=x，则DC=6-x，
则AC²=AD²+CD²，
x²=4²+（6-x）²，
解得：x=

13

3

，
BC=

13

3

，CO=10-

13

3

=

17

3

，
故相遇时警察的坐标为：（-

17

3

，0）．
故答案为：（-

17

3

，0）．

点评：此题主要考查了勾股定理的应用，根据题意得出BC的长是解题关键．