题目内容
已知:a2-b2=(a-b)(a+b); a3-b3=(a-b)(a2+ab+b2);a4-b4=(a-b)(a3+a2b+ab2+b3);按此规律,则:
(1)a5-b5=(a-b)( );
(2)若a-
=3,请你能根据上述规律求出代数式a3-
的值.
(1)a5-b5=(a-b)(
(2)若a-
| 1 |
| a |
| 1 |
| a3 |
考点:因式分解-运用公式法
专题:规律型
分析:(1)根据题意,按同一个字母的降幂排列直至不含这个字母为止;
(2)根据规律,先把代数式a3-
分解因式,再代入计算即可.
(2)根据规律,先把代数式a3-
| 1 |
| a3 |
解答:解:(1)∵a2-b2=(a-b)(a+b);
a3-b3=(a-b)(a2+ab+b2);
a4-b4=(a-b)(a3+a2b+ab2+b3);
∴a5-b5=(a-b)(a4+a3b+a2b2+ab3+b4);
故答案为:a4+a3b+a2b2+ab3+b4;
(2)a3-
=(a-
)(a2+1+
),
=(a-
)(a2-2+
+3),
=(a-
)[(a-
)2+3],
=3×(9+3),
=36.
a3-b3=(a-b)(a2+ab+b2);
a4-b4=(a-b)(a3+a2b+ab2+b3);
∴a5-b5=(a-b)(a4+a3b+a2b2+ab3+b4);
故答案为:a4+a3b+a2b2+ab3+b4;
(2)a3-
| 1 |
| a3 |
| 1 |
| a |
| 1 |
| a2 |
=(a-
| 1 |
| a |
| 1 |
| a2 |
=(a-
| 1 |
| a |
| 1 |
| a |
=3×(9+3),
=36.
点评:本题考查了平方差公式,是一道信息给予题,读懂信息是解题的关键.

练习册系列答案
相关题目
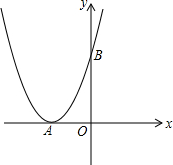 如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.
如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.