题目内容
如图,在 中
中 ,
, .点
.点 是线段
是线段 边上的一动点(不含
边上的一动点(不含 、
、 两端点),连结
两端点),连结 ,作
,作 ,交线段
,交线段 于点
于点 .
.

(1)求证: ∽
∽ ;
;
(2)设 ,
, ,请写
,请写 与
与 之间的函数关系式,并求
之间的函数关系式,并求 的最小值。
的最小值。
(3) 点在运动的过程中,
点在运动的过程中, 能否构成等腰三角形?若能,求出
能否构成等腰三角形?若能,求出 的长;若不能,请说明理由。
的长;若不能,请说明理由。
【答案】
(1)证明两个三角形相似,可以证明两个角相等。
(2)当 ,
, 有最小值是
有最小值是
(3)
【解析】
试题分析:(1)证明:

又
∴

∴
∴ ∽
∽
∵ ∽
∽
∴
即
∴ (
( )
)

∴当 ,
, 有最小值是
有最小值是
(3)∵ 是
是 的外角
的外角
∴
∵
∴
∴
当 时,
时,
得 ≌
≌
∴
当 时,
时,

∴ ∽
∽
∴
即:
∴
∴ 为等腰三角形时,
为等腰三角形时, 。
。
考点:相似三角形的性质,全等三角形的性质,二次函数求最值的问题,等腰三角形的性质
点评:此题比较综合,难度相对较难。动点问题在中考中,是压轴题,是出卷者区分优秀学生的题目,学生可以在平时的练习加强训练中,提升解此类题的能力。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


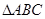 中,
中, ,
, 的平分线交
的平分线交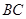 于
于 ,
, ,垂足为
,垂足为 ,连结
,连结 ,交
,交 于点
于点 .
. 
 ;
; ∥
∥ ,连结
,连结 ,猜想四边形
,猜想四边形 是什么图形?并证明你的猜想.
是什么图形?并证明你的猜想. 中,
中, ,
, 的垂直平分线
的垂直平分线 交
交 ,交
,交 于点
于点 ,点
,点 在
在 .
.
 是平行四边形.
是平行四边形. 满足什么条件时,四边形
满足什么条件时,四边形 中,
中, ,
, 的平分线交
的平分线交 于
于 ,
, ,垂足为
,垂足为 ,连结
,连结 ,交
,交 于点
于点 .
. 
 ;
; ∥
∥ ,连结
,连结 ,猜想四边形
,猜想四边形 是什么图形?并证明你的猜想.
是什么图形?并证明你的猜想.