题目内容
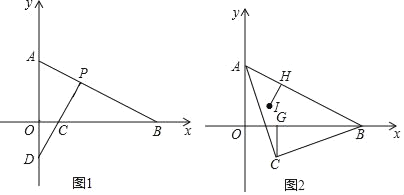
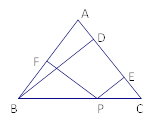
【题目】如图,已知△ABC中,AB=AC=![]() ,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
(1)求线段BF的长;
(2)求AE:EC的值.

【答案】(1)![]() ;(2)5.
;(2)5.
【解析】分析:(1)作AH⊥BC于H,如图,利用等腰三角形的性质得BH=CH=![]() BC=2,再利用勾股定理计算出AH=4,然后证明Rt△FBD∽Rt△ABH,再利用相似比计算BF和DF的长;
BC=2,再利用勾股定理计算出AH=4,然后证明Rt△FBD∽Rt△ABH,再利用相似比计算BF和DF的长;
(2)作CG∥AB交DF于G,如图,利用CG∥BD得到![]() =
=![]() =
=![]() ,然后由CG∥AD,根据平行线分线段成比例定理得到AE:EC的值.
,然后由CG∥AD,根据平行线分线段成比例定理得到AE:EC的值.
详解:(1)作AH⊥BC于H,如图,
∵AB=AC=![]() ,∴BH=CH=
,∴BH=CH=![]() BC=2.
BC=2.
在Rt△ABH中,AH=![]() =4.
=4.
∵DF垂直平分AB,∴BD=![]() ,∠BDF=90°.
,∠BDF=90°.
∵∠ABH=∠FBD,∴Rt△FBD∽Rt△ABH,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴BF=5,DF=2![]() ;
;
(2)作CG∥AB交DF于G,如图,
∵BF=5,BC=4,∴CF=1.
∵CG∥BD,∴![]() =
=![]() =
=![]() .
.
∵CG∥AD,∴![]() =
=![]() =
=![]() =5.
=5.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目