题目内容
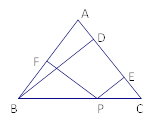
【题目】如图,在△ABC中,AB=AC,P为BC边上任意一点,PF⊥AB于F,PE⊥AC于E,若AC边上的高BD=a.
(1)试说明PE+PF=a;
(2)若点P在BC的延长线上,其它条件不变,上述结论还成立吗?如果成立请说明理由;如果不成立,请重新给出一个关于PE,PF,a的关系式,不需要说明理由.
【答案】(1)详见解析;(2)PF-PE=a,理由详见解析.
【解析】
(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,利用三角形的面积公式结合AB=AC即可证得结论;(2)PF-PE=a,根据题意画出图形,连接AP,则S△ABC=S△ABP+S△ACP,利用三角形的面积公式结合AB=AC即可证得结论.
(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,
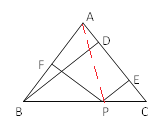
∴![]() ACBD=
ACBD=![]() ABPF+
ABPF+![]() ACPE,
ACPE,
∵AB=AC,
∴BD=PE+PF=a;
(2)PF-PE=a,理由如下:
连接AP,则S△ABC=S△ABP-S△ACP,
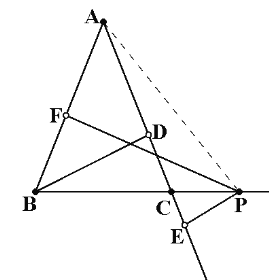
∴![]() ACBD=
ACBD=![]() ABPF-
ABPF-![]() ACPE,
ACPE,
∵AB=AC,
∴BD=PF-PE=a.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目