题目内容
【题目】已知:在平面直角坐标系中A(0,a)、B(b,0),且满足4(a﹣2)2+![]() (b﹣4)2=0,点P(m,m)在线段AB上
(b﹣4)2=0,点P(m,m)在线段AB上
(1)求A、B的坐标;
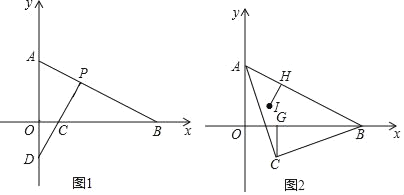
(2)如图1,若过P作PC⊥AB交x轴于C,交y轴交于点D,求![]() 的值;
的值;
(3)如图2,以AB为斜边在AB下方作等腰直角△ABC,CG⊥OB于G,设I是∠OAB的角平分线与OP的交点,IH⊥AB于H.请探究![]() 的值是否发生改变,若不改变请求其值;若改变请说明理由.
的值是否发生改变,若不改变请求其值;若改变请说明理由.
【答案】(1)A(0,2),B(4,0);(2)5;(3)![]() 的值不变,为2.
的值不变,为2.
【解析】
(1)根据非负数的性质即可解决问题.
(2)先求出直线AB的解析式,利用方程组求出点P坐标,再求出直线PC的解析式,求出点C坐标即可解决问题.
(3)如图2中,作IE⊥OA于E,CM⊥y轴于M,IF⊥OB于F.由△ACM≌△BCG,推出AM=BG,CM=CG,推出BH﹣AH=OB﹣OA=2CG,即可解决问题.
(1)∵4(a﹣2)2+![]() (b﹣4)2=0,
(b﹣4)2=0,
又∵4(a﹣2)2≥0,![]() (b﹣4)2≥0,
(b﹣4)2≥0,
∴a=2,b=4,
∴A(0,2),B(4,0).
(2)如图中,
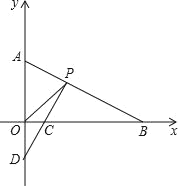
∵A(0,2),B(4,0),
∴直线AB的解析式为y=﹣![]() x+2,
x+2,
∵P(m,m),
∴点P在直线y=x上,
由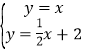 解得
解得![]() ,
,
∴点P(![]() ,
,![]() ),
),
∵PC⊥AB,
∴直线PC的解析式为y=2x﹣![]() ,
,
∴点C坐标为(![]() ,0),
,0),
∴OC=![]() ,BC=
,BC=![]() ,
,
∴![]() =
=![]() =5.
=5.
(3)![]() 的值不变.理由如下:
的值不变.理由如下:
如图2中,作IE⊥OA于E,CM⊥y轴于M,IF⊥OB于F.
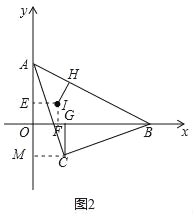
∵设I是∠OAB的角平分线与OP的交点,OP平分∠AOB,
∴I是内心,
∵IH⊥AB,IE⊥OA,IF⊥OB,
∴IE=IH=IF,易知AH=AE,BF=BH,
∴BH﹣AH=BF﹣AE=OB﹣OA,
∵∠MCG=∠ACB=90°,
∴∠ACM=∠BCG,
在△ACM和△BCG中,
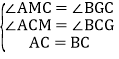 ,
,
∴△ACM≌△BCG(AAS),
∴AM=BG,CM=CG,
∵∠OMC=∠OGC=∠MOG=90°,
∴四边形OMCG是矩形,
∵CM=CG,
∴四边形OMCG是正方形,
∴OM=OG=CG=CM,
∴BH﹣AH=OB﹣AO=(BG+OG)﹣(AM﹣OM)=2CG,
∴![]() =
=![]() =2.
=2.

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案