题目内容
12.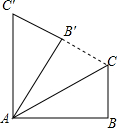 如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,此时AC′∥BC,C′B′的延长线过C点,则∠BAC的度数为( )
如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,此时AC′∥BC,C′B′的延长线过C点,则∠BAC的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先证明△AB′C′≌△AB′C,从而可得到∠CAB′=∠C′AB′,然后由旋转的性质可得到∠CAB=∠C′AB′,最后依据∠BAC′=90°可求得∠BAC的度数.
解答 解:由旋转的性质可知:AC=AC′,∠CAB=∠C′AB′,∠AB′C′=∠ABC=90°.
∵∠AB′C′=90°,
∴∠AB′C′=∠AB′C=90°.
在Rt△AB′C′和Rt△AB′C中,$\left\{\begin{array}{l}{AB′=AB′}\\{AC′=AC}\end{array}\right.$,
∴Rt△AB′C′≌Rt△AB′C.
∴∠C′AB′=∠CAB′.
∴∠C′AB′=∠CAB′=∠CAB.
∵AC′∥BC,∠B=90°,
∴∠BAC′=90°.
∴∠BAC=$\frac{1}{3}$×90°=30°.
故选:D.
点评 本题主要考查的是旋转的性质、全等三角形的性质和判定,熟练掌握旋转的性质是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
2.已知点A(a,b)在第一象限,那么点B(-b,-a)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.某市区现行出租车的收费标准:起步价5元(即行驶距离不超过3千米都需付5元车费),超过3千米后,每增加1千米,加收1.5元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费11元,那么甲地到乙地路程的最大值是( )
| A. | 5千米 | B. | 7千米 | C. | 8千米 | D. | 9千米 |
7.下列各数中,是整数的是( )
| A. | 0.2 | B. | 2-2 | C. | -4 | D. | $\sqrt{2}$ |
17.某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
| A. | 极差是6 | B. | 众数是10 | C. | 平均数是9.5 | D. | 方差是16 |
4.有一篮苹果平均分给几个人,若每人分2个,则还余下2个苹果,若每人分3个,则还少7个苹果,设有x个人分苹果,则可列方程为( )
| A. | 3x+2=2x+7 | B. | 2x+2=3x+7 | C. | 3x-2=2x-7 | D. | 2x+2=3x-7 |
1.下列运算正确的是( )
| A. | a3•a=a3 | B. | (-2a2)3=-6a5 | C. | a5+a5=a10 | D. | 8a5b2÷2a3b=4a2b |
4.下列各式能用平方差公式的是( )
| A. | (2a-b)(-b+2a) | B. | (-m-n)(-m+n) | C. | (a+b-c)(a+b-c) | D. | (a2-b)(b-a2) |



