题目内容
2.设方程:x2+3x-5=0的两个实数根为x1、x2,不解方程,求下列代数式的值:(1)$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$;
(2)x12+x22.
分析 (1)根据韦达定理得出x1+x2=-3,x1x2=-5,再求出x1-x2=±$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=±$\sqrt{(-3)^{2}-4×(-5)}$=$±\sqrt{29}$,代入$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=$\frac{-({x}_{1}-{x}_{2})}{{x}_{1}{x}_{2}}$即可得;
(2)x12+x22=(x1+x2)2-4x1x2即可得.
解答 解:(1)∵方程:x2+3x-5=0的两个实数根为x1、x2,
∴x1+x2=-3,x1x2=-5,
∴x1-x2=±$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=±$\sqrt{(-3)^{2}-4×(-5)}$=$±\sqrt{29}$,
则$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=$\frac{-({x}_{1}-{x}_{2})}{{x}_{1}{x}_{2}}$=$\frac{±\sqrt{29}}{-3}$=$±\frac{\sqrt{29}}{3}$;
(2)x12+x22=(x1+x2)2-4x1x2
=(-3)2-4×(-5)
=29.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,则x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
 解不等式组$\left\{\begin{array}{l}{3x+1<7}\\{2(x+1)-1≤3x+2}\end{array}\right.$,将解集在数轴上表示出来,并写出它的非负整数解.
解不等式组$\left\{\begin{array}{l}{3x+1<7}\\{2(x+1)-1≤3x+2}\end{array}\right.$,将解集在数轴上表示出来,并写出它的非负整数解.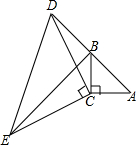 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作等腰直角三角形CDE,其中∠DCE=90°,连接BE. 如图是几个正方体所组成的几何体的俯视图,小正方形中的数字表示该位置小正方块的个数.请画出这个几何体的主视图和左视图.
如图是几个正方体所组成的几何体的俯视图,小正方形中的数字表示该位置小正方块的个数.请画出这个几何体的主视图和左视图. 如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为12m,
如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为12m,