��Ŀ����
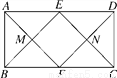
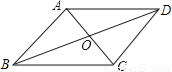
��ͼ���ھ���ABCD�У�AD��2AB����E��F�ֱ���AD��BC���е㣬����AF��BE��CE��DF�ֱ��ڵ�M��N���㣬���ı���EMFN��(����)
A. ������ B. ���� C. ���� D. ��ȷ��
A �����������ı���ABCDΪ���Σ� ��AD��BC��AD=BC�� �֡�E��F�ֱ�ΪAD��BC�е㣬 ��AE��BF,AE=BF,ED��CF��DE=CF�� ���ı���ABFEΪƽ���ı��Σ��ı���BFDEΪƽ���ı��Σ� ��BE��FD,��ME��FN�� ͬ����֤EN��MF�� ���ı���EMFNΪƽ���ı��Σ� ���ı���ABFEΪƽ���ı��Σ���ABCΪֱ�ǣ� ...
��ϰ��ϵ�д�
�����Ŀ


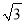 D. 1��
D. 1��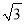
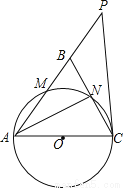
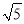 ��sin��BCP=
��sin��BCP=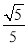 �����B��AC�ľ��룮
�����B��AC�ľ��룮